Question

Two stationary particles of masses ${{M}_{1}}$ and ${{M}_{2}}$ are at distance d apart. A third particle, lying on the line joining the particles, experiences no resultant gravitational force. The distance of this particle from ${{M}_{1}}$ is
$\text{A}\text{. }d\left( \dfrac{\sqrt{{{M}_{2}}}}{\sqrt{{{M}_{1}}}-\sqrt{{{M}_{2}}}} \right)$
$\text{B}\text{. }d\left( \dfrac{\sqrt{{{M}_{1}}}}{\sqrt{{{M}_{1}}}+\sqrt{{{M}_{2}}}} \right)$
$\text{C}\text{. }d\left( \dfrac{\sqrt{{{M}_{1}}}}{\sqrt{{{M}_{1}}}-\sqrt{{{M}_{2}}}} \right)$
$\text{D}\text{. }d\left( \dfrac{\sqrt{{{M}_{2}}}}{\sqrt{{{M}_{1}}}+\sqrt{{{M}_{2}}}} \right)$

Answer 1

Hint: Use the formula for gravitational force between two bodies i.e. $F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}$. Find the gravitational forces exerted on the third particles by both the particles. Then equate the two forces because the net force on the third particle is zero.
Formula used:
$F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}$

Complete answer:
Let us first understand the universal law of gravitation. According to universal law of gravitation, any two bodies in the universe exert forces of attraction on each other. Suppose there two bodies, whose masses are ${{m}_{1}}$ and ${{m}_{2}}$ and the distance between their centres is r, then the magnitude of the force of gravity exerted on one body by another is given as $F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}$.
Here, G is a proportionality constant called the universal gravitational constant.
The direction of gravitational force is always towards the body that exerts the force.

In the given question, there are two particles of masses ${{M}_{1}}$ and ${{M}_{2}}$. Both these particles are separated by a distance d.
It is given that a third particle is placed in between the two particles. Let the mass of the third particle be m and let it be placed at a distance of x from the ${{M}_{1}}$.

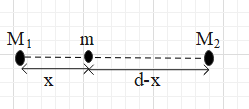
We know that both the masses ${{M}_{1}}$ and ${{M}_{2}}$ will exert forces on the third particle. However, it is given that the third particle experiences no force. This means that the two masses exert two forces on the third particle in such a way that the resultant force on it is zero.

If you see the given figure, the force exerted on the third particle by ${{M}_{1}}$ is ${{F}_{1}}=\dfrac{G{{M}_{1}}m}{{{x}^{2}}}$.
The direction of the force ${{F}_{1}}$ is towards ${{M}_{1}}$, i.e. towards left.
The force exerted on the third particle by ${{M}_{2}}$ is ${{F}_{2}}=\dfrac{G{{M}_{2}}m}{{{\left( d-x \right)}^{2}}}$.

The direction of the force ${{F}_{2}}$ is towards ${{M}_{2}}$, i.e. towards right.
For the resultant force on the third particle to be zero, ${{F}_{1}}={{F}_{2}}$.
$\Rightarrow \dfrac{G{{M}_{1}}m}{{{x}^{2}}}=\dfrac{G{{M}_{2}}m}{{{\left( d-x \right)}^{2}}}$
$\Rightarrow \dfrac{{{M}_{1}}}{{{x}^{2}}}=\dfrac{{{M}_{2}}}{{{\left( d-x \right)}^{2}}}$
Take square roots on both the sides.
$\Rightarrow \dfrac{\sqrt{{{M}_{1}}}}{x}=\pm \dfrac{\sqrt{{{M}_{2}}}}{\left( d-x \right)}$
Therefore, $\dfrac{\sqrt{{{M}_{1}}}}{x}=\dfrac{\sqrt{{{M}_{2}}}}{\left( d-x \right)}$ or $\dfrac{\sqrt{{{M}_{1}}}}{x}=-\dfrac{\sqrt{{{M}_{2}}}}{\left( d-x \right)}$.
However, $\sqrt{{{M}_{1}}}$, $\sqrt{{{M}_{2}}}$, x are positive because masses and distances are always positive.

Since d > x, d-x is also positive.

Therefore, $\dfrac{\sqrt{{{M}_{1}}}}{x}$ and $\dfrac{\sqrt{{{M}_{2}}}}{\left( d-x \right)}$ both are positive.
 This means that the equation $\dfrac{\sqrt{{{M}_{1}}}}{x}=-\dfrac{\sqrt{{{M}_{2}}}}{\left( d-x \right)}$ is not true and let us it discard it.

Therefore, $\dfrac{\sqrt{{{M}_{1}}}}{x}=\dfrac{\sqrt{{{M}_{2}}}}{\left( d-x \right)}$.
$\Rightarrow \left( d-x \right)\sqrt{{{M}_{1}}}=x\sqrt{{{M}_{2}}}$
$\Rightarrow d\sqrt{{{M}_{1}}}-x\sqrt{{{M}_{1}}}=x\sqrt{{{M}_{2}}}$
$\Rightarrow d\sqrt{{{M}_{1}}}=x\left( \sqrt{{{M}_{1}}}+\sqrt{{{M}_{2}}} \right)$
$\Rightarrow x=d\left( \dfrac{\sqrt{{{M}_{1}}}}{\left( \sqrt{{{M}_{1}}}+\sqrt{{{M}_{2}}} \right)} \right)$
Therefore, the third particle is situated at a distance of $d\left( \dfrac{\sqrt{{{M}_{1}}}}{\left( \sqrt{{{M}_{1}}}+\sqrt{{{M}_{2}}} \right)} \right)$ from the particle of mass ${{M}_{1}}$.

So, the correct answer is “Option B”.

Note:
Other than taking the square roots of the expressions in equation $\dfrac{{{M}_{1}}}{{{x}^{2}}}=\dfrac{{{M}_{2}}}{{{\left( d-x \right)}^{2}}}$ we can also write a quadratic equation for x and solve it using the quadratic formula or the completing the square method.
Note that in this case x cannot be a negative value. Negative value of x means that the third particle is placed at a point that is not in between the other two particles. However, at this position both forces acting on the particle will be in the same direction and thus the net force will not be zero.