Question

Two square plates $ l \times l $ and dielectric $ \left( {\dfrac{l}{2} \times \dfrac{t}{2} \times l} \right) $ are arranged in figure. Find the equivalent capacitance of the structure.

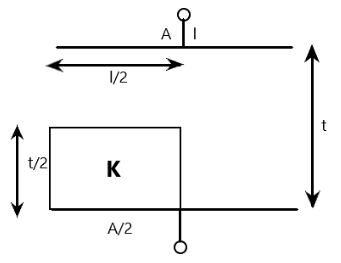
(A) $ \dfrac{{{\varepsilon _0}A}}{t}\left( {\dfrac{{3K + 1}}{{2\left( {K + 1} \right)}}} \right) $
(B) $ \dfrac{{2{\varepsilon _0}A}}{t}\left( {\dfrac{{K + 1}}{{\left( {K + 3} \right)}}} \right) $
(C) $ \dfrac{{{\varepsilon _0}A}}{t}\left( {\dfrac{{K + 1}}{{\left( {K + 3} \right)}}} \right) $
(D) $ \dfrac{{{\varepsilon _0}A}}{t}\left( {\dfrac{{2K + 1}}{{2K + 3}}} \right) $

Answer 1

Hint: The system acts like three capacitors in general. The capacitor with the dielectric, the capacitor without the dielectric (which ends where the dielectric ends) just above the dielectric, and the capacitor right of them both. The dielectric capacitor and the capacitor above it are in series, and the one on the right is in parallel to them.

Formula used: In this solution we will be using the following formulae;
 $ C = \dfrac{{{\varepsilon _o}A}}{d} $ where $ C $ is the capacitance of a capacitor without a dielectric, $ {\varepsilon _o} $ is the permittivity of free space, $ A $ is the area of the plate of the capacitor and $ d $ is the separation.
 $ {C_d} = \dfrac{{K{\varepsilon _o}A}}{d} $ where $ {C_d} $ is the capacitance of a capacitor with dielectric, and $ K $ is the dielectric constant of the dielectric.
  $ \dfrac{1}{{{C_{eqs}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} $ where $ {C_{eqs}} $ is the effective capacitance of two capacitors in series, $ {C_1} $ and $ {C_2} $ are the individual capacitance of series capacitors.
 $ {C_{eqp}} = {C_1} + {C_2} $ where $ {C_{eqp}} $ is the equivalent capacitance of two capacitors in parallel, and $ {C_1} $ and $ {C_2} $ are the individual capacitors in parallel.

Complete Step-by-Step solution:

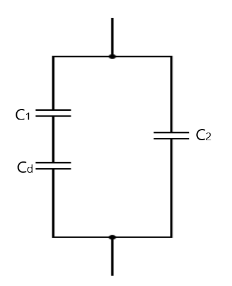
To answer this, we note that the dielectric will act as a capacitor which is in series to a capacitor of free space above it, as seen in the diagram above.
The capacitance of a capacitor with dielectric can be given as
 $ {C_d} = \dfrac{{K{\varepsilon _o}A}}{d} $ where $ K $ is the dielectric constant of the dielectric, $ {\varepsilon _o} $ is the permittivity of free space, $ A $ is the area of the plate of the capacitor and $ d $ is the separation.
For this dielectric, as seen from question, it would be
 $ {C_d} = \dfrac{{K{\varepsilon _o}\dfrac{A}{2}}}{{\dfrac{t}{2}}} = \dfrac{{K{\varepsilon _0}A}}{t} $
Capacitors without dielectric is given by
 $ C = \dfrac{{{\varepsilon _o}A}}{d} $
Hence, for the capacitor $ {C_1} $ , we have
 $ {C_1} = \dfrac{{{\varepsilon _o}\dfrac{A}{2}}}{{\dfrac{t}{2}}} = \dfrac{{{\varepsilon _0}A}}{t} $
The equivalent capacitance of capacitors in series is given as
 $ \dfrac{1}{{{C_{eqs}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} $ where $ {C_1} $ and $ {C_2} $ are the individual capacitance of series capacitors.
Hence, for $ {C_d} $ and $ {C_1} $ , we have
 $ \dfrac{1}{{{C_{eqs}}}} = \dfrac{t}{{{\varepsilon _0}A}} + \dfrac{t}{{K{\varepsilon _0}A}} = \dfrac{{t(K + 1)}}{{K{\varepsilon _0}A}} $
 $ \Rightarrow {C_{eqs}} = \dfrac{{K{\varepsilon _0}A}}{{t(K + 1)}} $
This capacitor is now in parallel with the capacitor $ {C_2} $
 $ {C_2} $ can be given as
 $ {C_2} = \dfrac{{{\varepsilon _o}\dfrac{A}{2}}}{t} = \dfrac{{{\varepsilon _0}A}}{{2t}} $
Capacitors in parallel is given as
 $ {C_{eqp}} = {C_1} + {C_2} $ where $ {C_1} $ and $ {C_2} $ are the individual capacitors in parallel.
Hence,
 $ {C_{eqv}} = {C_{eqs}} + {C_2} = \dfrac{{K{\varepsilon _0}A}}{{t(K + 1)}} + \dfrac{{{\varepsilon _0}A}}{{2t}} $
Hence, we have
 $ \Rightarrow {C_{eqv}} = \dfrac{{2K{\varepsilon _0}A + K{\varepsilon _0}A + {\varepsilon _0}A}}{{2t(K + 1)}} = \dfrac{{{\varepsilon _0}A}}{t}\left( {\dfrac{{3K + 1}}{{2(K + 1)}}} \right) $
Hence, the correct option is A.

Note:
For clarity, even though the dielectric does not have a plate, to cover it as a normal capacitor, it still behaves as a normal capacitor. This is because capacitors in series, for example, only one of the plates of one capacitor will be connected to the voltage source. Hence, without unconnected plates, the capacitors behave just the same.