Question

Two springs have force constants \[{{k}_{1}}\] and \[{{k}_{2}}\]. They are attached to mass \[\text{m}\] and two fixed supports.

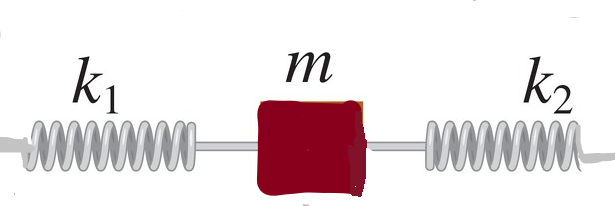
If the surface is frictionless, find frequency of oscillations and spring factors of the combination.

Answer 1

Hint:Firstly, separate values of restoring forces \[{{\text{F}}_{1}}\] and \[{{\text{F}}_{2}}\] for springs \[1\] and \[2\] is calculated and then total restoring force is obtained.
Comparing it with the standard equation gives the value of force constant \[k\] and then frequency is calculated.

Formula used \[\text{F = }-ky\], \[f=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}}\]

Complete Step by step solution
When mass \[\text{m}\] is displaced through some distance, say \[y\] towards spring on left, it will get compressed and the other one on the right will get elongated.
But the restoring forces \[{{\text{F}}_{1}}\] and \[{{\text{F}}_{2}}\] developed in the two springs will be towards right that is in the same direction.
As \[{{k}_{1}}\] and \[{{k}_{2}}\] are force constants of the two springs, therefore
\[{{\text{F}}_{1}}=-{{k}_{1}}y\] and \[{{\text{F}}_{2}}=-{{k}_{2}}y\]
Total restoring force
\[\begin{align}
  & \text{F = }{{\text{F}}_{1}}\text{+ }{{\text{F}}_{2}} \\
 & \text{F = }-{{k}_{1}}\text{y}-{{k}_{2}}\text{y} \\
\end{align}\]
\[\text{F = }-\left( {{k}_{1}}+{{k}_{2}} \right)\text{y}\] …..(1)
In the given arrangement,
\[\text{F = }-ky\] …..(2)
From equation (1) and (2), we get
\[k={{k}_{1}}+{{k}_{2}}\]
Hence, frequency of oscillation of given spring system can be calculated as:
\[\begin{align}
  & v=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}} \\
 & v=\dfrac{1}{2\pi }\sqrt{\dfrac{{{k}_{1}}+{{k}_{2}}}{m}} \\
\end{align}\]

Note Knowledge of concepts regarding motion of loaded spring should be there. Restoring force, which acts on a body to bring back its equilibrium position. The formula used is \[\text{F = }-ky\], where \[\text{F}\]is restoring force, \[k\] is force constant and \[y\] is displacement.