Question

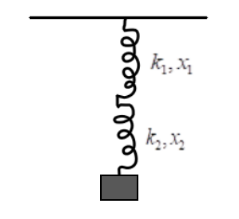
Two springs are in series combination and are attached to a block of mass $ m $ which is in equilibrium. The spring constants and the extensions in the springs are shown in the figure then the force exerted by the spring on the block is

(A) $ \dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}}\left( {{x_1} + {x_2}} \right) $
(B) $ {k_1}{x_1} + {k_2}{x_2} $
(C) $ {k_1}{x_1} $
(D) None of these

Answer 1

Hint: Based on Hooke’s law the total force exerted on the block will be equal to the extension of both strings, and the effective spring constant. The springs are in series, the effective force constant is the inverse of the sum of the inverse of the individual spring constant or the inverse of the effective force constant is equal to the sum of the inverse of each of the spring constants.

Formula used In this solution we will be using the following formulae;
 $ F = ke $ where $ F $ is the force exerted by a spring, $ k $ is the force constant, and $ e $ is the extension of spring.
 $ \dfrac{1}{{{k_{eqs}}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} $ where $ {k_{eqs}} $ is the equivalent spring constant of two springs in series, $ {k_1} $ is the spring constant of one, and $ {k_2} $ is the spring constant of the other.

Complete Step-by-Step solution:
To solve this question, we note that the two springs are in series. And that the force exerted by such a spring could be considered as the product of an effective spring constant and the total extension in the springs. Generally, the force exerted by a spring is
 $ F = ke $ where $ F $ is the force exerted by a spring, $ k $ is the force constant, and $ e $ is the extension of spring.
Then, for the combination of springs in series, we have
 $ F = {k_{eqs}}e $ where $ {k_{eqs}} $ is the effective force constant of the network. This in itself, is given by
 $ \dfrac{1}{{{k_{eqs}}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} $ where $ {k_{eqs}} $ is the equivalent spring constant of two springs in series, $ {k_1} $ is the spring constant of one, and $ {k_2} $ is the spring constant of the other.
Actually adding them, we have
 $ \dfrac{1}{{{k_{eqs}}}} = \dfrac{{{k_1} + {k_2}}}{{{k_1}{k_2}}} $
 $ \Rightarrow {k_{eqs}} = \dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}} $
Hence, the force exerted would be
 $ F = \dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}}\left( {{x_1} + {x_2}} \right) $
The correct option is A.

Note:
For clarity, the $ {x_1} + {x_2} $ is the extension of the springs in total. As seen in the diagram, the upper spring is extended by $ {x_1} $ , and the extension of the upper one is $ {x_2} $ , hence, the total extension would be the addition of them both.