Question

Two spherical bodies of masses M and 5M and radii R and 2R, respectively, are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smaller body just before collision is?
A. 2.5R
B. 4.5R
C. 7.5R
D. 1.5R

Answer 1

Hint: We will require the gravitational force formula: $F=\dfrac{G{{M}_{1}}{{M}_{2}}}{{{R}^{2}}}$ and equate it using the equation $F=Ma$. Using this, we will find the acceleration of the bodies. Then, we will use the newton’s law of motion: $s=ut+\dfrac{1}{2}a{{t}^{2}}$ to find the distances travelled by the bodies before the collision. We will then use the ratio of distances travelled before collision and find it using the information given regarding the distance between the centres of the bodies being 12R.

Step by step solution:
Let’s start by making a detailed diagram of the problem.

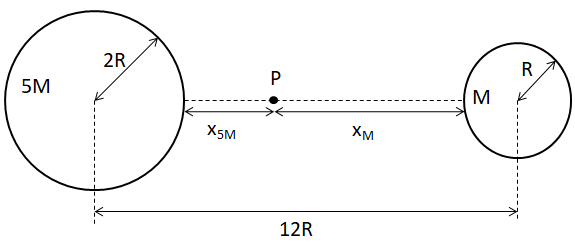
The spherical body of mass 5M has a radius of 2R and the body of mass M has a radius of M. The distance from the centre of the body of mass M till the body of mass 5M is given to be 12R. The given system is in vacuum and no external force is applied to this system. Hence the only force acting between them is the attractive gravitational force. Let the position (P) be the point where the bodies collided with each other. The distance travelled by the body of mass 5M is ${{x}_{5M}}$and the distance travelled by the body of mass M is ${{x}_{M}}$.
The gravitational force is given by: $F=\dfrac{G{{M}_{1}}{{M}_{2}}}{{{R}^{2}}}$. We also know that force (F) is equal to the mass of the body (M) times acceleration of the body (a): $F=Ma\Rightarrow a=\dfrac{F}{M}$. Hence the acceleration of the body is proportional to the inverse of the mass of the body, that is: $a\propto \dfrac{1}{M}$.
Hence for the current case where we will consider the acceleration of the body of mass M to be: ${{a}_{M}}$ and the acceleration of the body of mass 5M to be ${{a}_{5M}}$; the ratio of the accelerations will be: $\dfrac{{{a}_{M}}}{{{a}_{5M}}}=\dfrac{5M}{M}\Rightarrow \dfrac{{{a}_{M}}}{{{a}_{5M}}}=5\Rightarrow {{a}_{M}}=5{{a}_{5M}}$. Hence the acceleration of the body of mass M is 5 times the acceleration of the body of mass 5M.
We will now use Newton's law of motion: $s=ut+\dfrac{1}{2}a{{t}^{2}}$. Let’s consider the case for the body of mass 5M: a=${{a}_{5M}}$, s=${{x}_{5M}}$and since we consider both the bodies to be initially at rest, hence u=0. Therefore, $s=ut+\dfrac{1}{2}a{{t}^{2}}\Rightarrow {{x}_{5M}}=0t+\dfrac{1}{2}{{a}_{5M}}{{t}^{2}}\Rightarrow {{x}_{5M}}=\dfrac{1}{2}{{a}_{5M}}{{t}^{2}}\to (1)$.
Similarly, when we consider the newton’s law of motion for the body of mass M, a=${{a}_{5M}}$, s=${{x}_{5M}}$and u=0 we get: $s=ut+\dfrac{1}{2}a{{t}^{2}}\Rightarrow {{x}_{M}}=0t+\dfrac{1}{2}{{a}_{M}}{{t}^{2}}\Rightarrow {{x}_{M}}=\dfrac{1}{2}{{a}_{M}}{{t}^{2}}\to (2)$.
Taking a ratio of the two equations, we find: \[\dfrac{(1)}{(2)}\Rightarrow \dfrac{{{x}_{5M}}}{{{x}_{M}}}=\dfrac{\dfrac{1}{2}{{a}_{5M}}{{t}^{2}}}{\dfrac{1}{2}{{a}_{M}}{{t}^{2}}}\Rightarrow \dfrac{{{x}_{5M}}}{{{x}_{M}}}=\dfrac{{{a}_{5M}}}{{{a}_{M}}}=\dfrac{1}{5}\Rightarrow {{x}_{M}}=5{{x}_{5M}}\]. Hence the amount of distance travelled by the body of mass M is 5 times the amount of distance travelled by the body of mass 5M.
We know that the distance 12R, is from the centre of each body to another. Hence, the net distance from the surface of each body to another is: $12R=2R+{{x}_{5M}}+{{x}_{M}}+R\Rightarrow 12R=3R+{{x}_{5M}}+{{x}_{M}}\Rightarrow 9R={{x}_{5M}}+{{x}_{M}}$.
Using the relation: \[{{x}_{M}}=5{{x}_{5M}}\], the above equation becomes $9R={{x}_{5M}}+{{x}_{M}}\Rightarrow 9R={{x}_{5M}}+5{{x}_{5M}}\Rightarrow 9R=6{{x}_{5M}}\Rightarrow {{x}_{5M}}=\dfrac{9R}{6}=1.5R$.
$\therefore {{x}_{5M}}=1.5R$and similarly, ${{x}_{M}}=7.5R$.
Therefore the distance travelled by the body with least mass (M) before collision is 7.5R.

Note: From the solution we can find that, the ratio of the distance travelled by the bodies is inversely proportional to the amount of distance travelled by each body. Hence, \[\dfrac{{{x}_{5M}}}{{{x}_{M}}}=\dfrac{{{a}_{5M}}}{{{a}_{M}}}=\dfrac{1}{5}\]for the current problem.