Question

Two sources of sound ${S_1}$ and ${S_2}$, emitting waves of equal wavelength $20.0{\text{ }}cm$, are placed with a separation of $20.0{\text{ }}cm$ between them. A detector can be moved on a line parallel to ${S_1}{S_{}}$ and at a distance of $20.0{\text{ }}cm$ from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through which the detector should be shifted to detect a minimum of sound.

Answer 1

Hint: First of all we have to construct a figure. We have to assume that the waves meet at D which is $x$ distance from O. From geometry we have to find the path difference. Also from the minimum condition of waves we have to find path differences. After that by equating both terms we will eventually have our result.

Complete step by step answer:

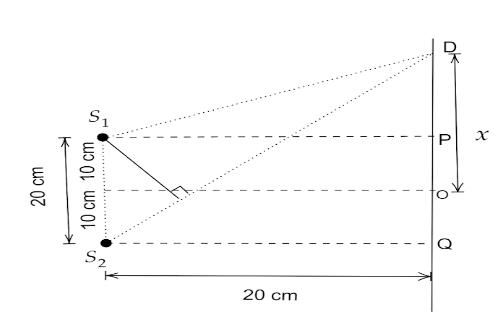
From the given figure we have to find out the phase difference $\Delta x$. According to given data $\lambda = 20\,cm$ and distance between $DQ$ and ${S_1}{S_2}$ is $20\,cm$ also ${S_1}{S_2} = 20{\text{ }}cm$. Let the distance between $D$ and $o$ is $x$ $cm$.
Then $PD = \left( {x - 10} \right)$ and $QD = \left( {x + 10} \right)$
From $\Delta {S_1}PD$ and $\Delta {S_2}QD$ we get,
${S_1}D = \sqrt {{{\left( {{S_1}P} \right)}^2} + {{\left( {PD} \right)}^2}} $ from Pythagoras Theorem,
$\Rightarrow {S_1}D = \sqrt {{{\left( {20} \right)}^2} + {{\left( {x - 10} \right)}^2}} $ and
$\Rightarrow {S_2}D = \sqrt {{{\left( {{S_2}Q} \right)}^2} + {{\left( {QD} \right)}^2}} $
$\Rightarrow {S_2}D = \sqrt {{{\left( {20} \right)}^2} + {{\left( {x + 10} \right)}^2}} $

The path difference $\Delta x$ is,
$\Delta x$=${S_2}D$-${S_1}D$
$ \Rightarrow \Delta x = \sqrt {{{\left( {20} \right)}^2} + {{\left( {x + 10} \right)}^2}} - \sqrt {{{\left( {20} \right)}^2} + {{\left( {x - 10} \right)}^2}} - - - - - \left( 1 \right)$
Path difference is defined as,
$\Delta x = \dfrac{{(2n + 1)\lambda }}{2}$
For minima, $n = 0$
$\therefore \Delta x = \dfrac{\lambda }{2}$
Substituting the value $\lambda $ we get,
$\Delta x = \dfrac{{20}}{2} = 10 - - - - \left( 2 \right)$

From equation $\left( 1 \right)$ and $\left( 2 \right)$ we get,
$\sqrt {{{\left( {20} \right)}^2} + {{\left( {x + 10} \right)}^2}} - \sqrt {{{\left( {20} \right)}^2} + {{\left( {x - 10} \right)}^2}} = 10$
$ \Rightarrow \sqrt {{{\left( {20} \right)}^2} + {{\left( {x + 10} \right)}^2}} = 10 + \sqrt {{{\left( {20} \right)}^2} + {{\left( {x - 10} \right)}^2}} $
Squaring both sides we get,
$400 + {x^2} + 100 + 20x = 100 + 400 + {x^2} - 20x + 100 + 20\sqrt {{{\left( {20} \right)}^2} + {{\left( {x - 10} \right)}^2}} $
By eliminating some terms we get,
$40x - 100 = 20\sqrt {{{\left( {20} \right)}^2} + {{\left( {x - 10} \right)}^2}} $
Again, squaring both sides we get,
$1600{x^2} + 10000 - 8000x = 400\left( {500 + {x^2} - 20x} \right) \\
\Rightarrow 1200{x^2} = 200000 $
Now the value of $x = 12.9$

Hence, the minimum distance through which the detector should be shifted to detect a minimum of sound is $12.9{\text{ }}cm$.

Note: We must use Pythagoras Theorem in the above figure. While solving the equations we must be sure that we do not cancel out any value of variable. For a minimum condition the value of $n = 0$.We have to assume that the waves meet $x$distance from the midpoint of detector $DQ$.