Question

Two solid cylinders P and Q of same mass and same radius start rolling down a fixed inclined plane from the same height at the same time. Cylinder P has most of its mass concentrated near its surface, while Q has most of its mass concentrated near the axis. Which statement(s) is (are) correct?

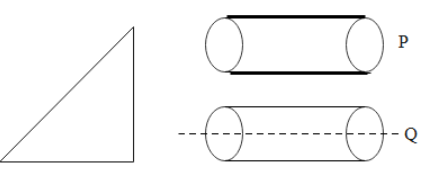
A. Both cylinders P and Q reach ground at the same time.
B. Cylinder P has larger linear acceleration than cylinder Q.
C. Both cylinders reach ground with the same translational kinetic energy.
D. Cylinder Q reaches the ground with larger angular speed.

Answer 1

Hint: First, we need to know which cylinder has greater moment of inertia based on the given mass distribution. Then using expressions relating the moment of inertia with the linear acceleration of the centre of mass of a cylinder rolling down an inclined plane, we can compare the linear accelerations of two cylinders. From this, we can further compare velocities of cylinders.
Formula used:
The formula for moment of inertia is
$I = m{r^2}$
For a cylinder which is rolling down an inclined plane, the acceleration of its centre of mass is given as
${a_c} = \dfrac{{g\sin \theta }}{I}\left( {1 + M{R^2}} \right)$
Kinetic energy is given as
$K = \dfrac{1}{2}m{v^2}$
The relation between linear velocity and the angular velocity is given as
$v = r\omega $

Complete answer:
We are given that two solid cylinders P and Q of same mass and same radius. Cylinder P has most of its mass concentrated near its surface, while Q has most of its mass concentrated near the axis. This means that the distribution of mass is different for two cylinders due to which we need to take the moment of inertia of the cylinders into consideration. As we know that moment of inertia is given as
$I = m{r^2}$
Here m is the mass of the object while r represents the distance of this mass from the axis of rotation. Since the axis of rotation of a cylinder is a line passing through the centre, this means that moment of inertia of cylinder P is greater than that of cylinder Q since r is large in case of cylinder P.
${I_P} > {I_Q}$
Now we know the expression for the linear acceleration of the centre of mass of a cylinder which is rolling down an inclined plane. For the two cylinders we can write the expressions in the following way.
$
  {a_{cP}} = \dfrac{{g\sin \theta }}{{{I_P}}}\left( {1 + M{R^2}} \right) \\
  {a_{cQ}} = \dfrac{{g\sin \theta }}{{{I_Q}}}\left( {1 + M{R^2}} \right) \\
 $
Therefore, linear acceleration is inversely proportional to the moment of inertia, so ${a_{cP}} < {a_{cQ}}$.
Now if acceleration of P is less than that of Q, then velocity of P will also be less than Q.
${v_P} < {v_Q}$
Different velocities mean that the cylinder Q will reach the round first.
Since translational kinetic energy is given as
$
  {K_P} = \dfrac{1}{2}mv_P^2 \\
  {K_Q} = \dfrac{1}{2}mv_Q^2 \\
 $
Therefore, ${K_P} < {K_Q}$
Similarly, we know the relation between the linear velocity and the angular velocity which is given as
$
  {v_P} = r{\omega _P} \\
  {v_Q} = r{\omega _Q} \\
 $
Therefore, ${\omega _P} < {\omega _Q}$

So,the correct answer is Option D.

Note:
Since the cylinders are rolling down the inclined plane, there is no friction between the surface and the cylinders. The total kinetic energy which is the sum of the translational and the rotational kinetic energy will remain the same.