Question

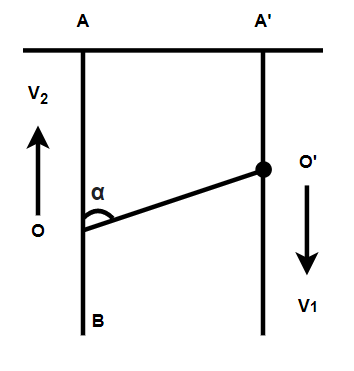
Two small rings $ O $ and $ O' $ are put on two vertical stationary rods $ AB $ and $ A'B' $ , respectively. One end of an inextensible thread is tied at the point $ A' $ . The thread passes through the ring $ O' $ and its other end is tied to the ring $ O $ . Assuming that ring $ O $ moves downwards at a constant velocity $ {v_1} $ , the velocity $ {v_2} $ of the ring $ O $ when $ \angle AOO' = \alpha $ is

 $ \left( A \right){\text{ }}{{\text{v}}_1}\left[ {\dfrac{{2{{\sin }^2}(\alpha /2)}}{{\cos \alpha }}} \right] $
 $ \left( B \right){\text{ }}{{\text{v}}_1}\left[ {\dfrac{{2{{\cos }^2}(\alpha /2)}}{{\sin \alpha }}} \right] $
 $ \left( C \right){\text{ }}{{\text{v}}_1}\left[ {\dfrac{{3{{\cos }^2}(\alpha /2)}}{{\sin \alpha }}} \right] $
 $ \left( D \right){\text{ None of these}} $

Answer 1

Hint: Since, in this question, we have an inextensible thread. Also since the reference frame is fixed to ring $ O $ . So in this system, the velocity of the ring will be equal to $ {v_1}/\cos \alpha $ and it will be directed upwards. So from this, we will be able to find the velocity of the ring $ O $ which will be relative to the straight line $ AA' $ .

Formula used:
The trigonometric identity used is,
 $ 1 - \cos \alpha = 2{\sin ^2}(\alpha /2) $ .

Complete step by step solution:
So for solving this question, we will go to the reference frame which is fixed to ring $ O' $ in the system, and from this, we will get the velocity of the ring will be equal to $ {v_1}/\cos \alpha $ . Since we know that the velocity of the ring $ O $ which will be relative to the straight line $ AA' $ is stationary with respect to the ground.
So from this, the equation made will be,
 $ \Rightarrow {v_1} = {v_1}\cos \alpha + {v_2}\cos \alpha $
Solving for the value of $ {v_2} $ , we will get the above equation as
 $ \Rightarrow {v_2} = \dfrac{{{v_1}\left( {1 - \cos \alpha } \right)}}{{\cos \alpha }} $
And as we know that $ 1 - \cos \alpha = 2{\sin ^2}(\alpha /2) $
So on substituting the values in the above equation, we will get the equation as
 $ \Rightarrow {v_2} = \dfrac{{{v_1}\left( {2{{\sin }^2}(\alpha /2)} \right)}}{{\cos \alpha }} $ .
Hence, the option $ \left( A \right) $ is correct.

Note:
For solving this type of question the most important thing is a figure, so a body diagram should always be made while solving this type of question as it makes the question very clear and also it makes precise which helps to find the required values quickly.