Question

Two small bodies of mass 10kg and 20kg are kept at a distance of 1.0m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases by 0.5m?

Answer 1

Hint: When two small bodies are interacting and mass and velocity is given then we have to use the concept of conservation of Energy for doing calculation of velocity. Here in this question initially only gravitational forces are interacting so only gravitational potential energy is used in this calculation.

Complete answer:
Here it is given in the question that two small bodies are of 10kg and 20 kg are kept 1m apart. It is already mentioned that only gravitational forces are acting that means no external force acts on the system. So according to Newton’s Second Law,
\[{{F}_{ext}}=\dfrac{dp}{dt}\].
As external forces are not acting so we will take external force as zero.
\[\begin{align}
  & \Rightarrow \dfrac{dp}{dt}=0 \\
 & \Rightarrow p=cons\tan t \\
\end{align}\]
So momentum remains conserved for that system.
Here initially both the bodies are not moving so initial linear momentum is zero and as momentum is conserved so final linear momentum will also get zero.

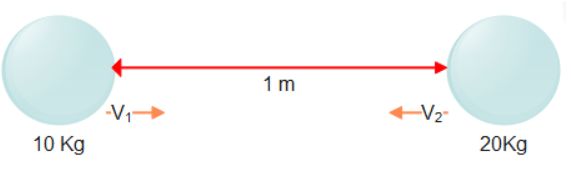
Let us suppose the velocity of 10Kg body is considered as \[{{V}_{1}}\] and that of velocity of 20Kg body is\[{{V}_{2}}\].
Since both the velocities are not equal in magnitude but opposite in direction.
Let us consider the direction of velocity of the ball 10 kg as positive. While that of 20kg is considered as negative.
So the momentum of a 20 kg ball is taken as negative.
So Initial linear momentum of the system is given as =\[10({{V}_{1}})-20({{V}_{2}})=0\].
\[\Rightarrow 10{{V}_{1}}=20{{V}_{2}}\]
\[\Rightarrow {{V}_{1}}=2{{V}_{2}}\]\[(Equation1)\]
Initial Gravitational Potential Energy can be calculated as
\[{{(G.P.E)}_{Initial}}=-\dfrac{G(10)(20)}{1}=-200G\]\[(Equation2)\]
Negative sign shows the attraction between two bodies.

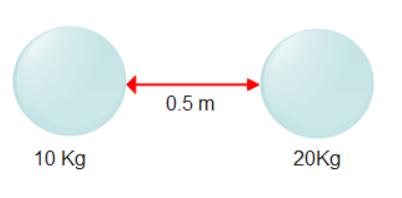
Final Gravitational Potential Energy can be calculated as
\[{{(G.P.E)}_{final}}=-\dfrac{G(10)(20)}{(0.5)}=-400G\]\[(Equation3)\]
Negative sign shows the attraction between two bodies.
According to Law of Conservation of Energy,
Initial Gravitational Potential Energy = Final Gravitational Potential Energy + Kinetic energy of two balls.
\[{{(G.P.E.)}_{Initial}}={{(G.P.E.)}_{Final}}+\dfrac{1}{2}(10){{V}_{1}}^{2}+\dfrac{1}{2}(20){{V}_{2}}^{2}\]
Put the value of Gravitational potential energy from equation 2 and 3
\[\Rightarrow \]\[-200G=-400G+\dfrac{1}{2}(10{{V}_{1}}^{2}+20{{V}_{2}}^{2})\]
\[\Rightarrow \]\[-13.34\times {{10}^{-9}}\]\[=-26.80\times {{10}^{-9}}\]\[+30{{V}_{2}}^{2}\]
\[\Rightarrow 13.46\times {{10}^{-9}}=30{{V}_{2}}^{2}\]
\[\Rightarrow {{V}_{2}}^{2}=4.48\times {{10}^{-10}}\]
\[\therefore {{V}_{2}}=2.1\times {{10}^{-5}}m{{s}^{-1}}\]
Put the value of V2 in equation 1, we get
\[\begin{align}
  & \Rightarrow {{V}_{1}}=2\times 2.1\times {{10}^{-5}} \\
 & \therefore {{V}_{1}}=4.1\times {{10}^{-5}}m{{s}^{-1}} \\
\end{align}\]
So final velocities of particle will be \[4.1\times {{10}^{-5}}m{{s}^{-1}}\And 2.1\times {{10}^{-5}}m{{s}^{-1}}\].

Note:
Direction of motion is also considered in this type of numerical. We should assume the direction of velocity as positive and negative according to our convenience. Sign only represents direction here, no need to use the sign in calculation. But the sign used in gravitational potential energy is considered numerical.