Question

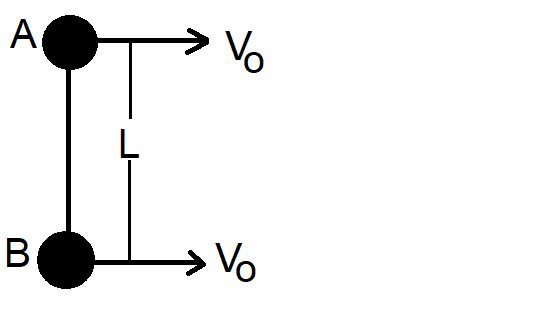
Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rod of length L. The system translates on a frictionless horizontal surface with a velocity ${{v}_{0}}$ ​ in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find:
a) the linear speeds of the balls A and B after the collision
b) the velocity of the centre of mass C of the system A+B+P and
c) the angular speed of the system about C after the collision

Answer 1

Hint: For solving this question, we must go part by part starting from A to C, because for solving each part, the data that we get from the previous part will be used. For A part, it can easily be solved using the law of conservation of momentum. After we get the relationship between the velocities, we can use that to solve part B for getting the velocity that is required. The key part for solving the C part is \[{{P}_{cm}}={{I}_{cm}}\times \omega \]

Complete answer:
Two balls of mass m, A and B respectively, are rigidly joined to the light ends of the rod of length L. The machine films in the direction perpendicular to the rod at a velocity ${{v}_{0}}$.
As the ball collides with the ball, a particle P of mass m held at rest on the surface adheres to ball A.
So,For the part A ,We have,
Just over its length can the light rod exert a force on the ball B.
But the impact won't change the speed.
B has velocity = ${{v}_{0}}$
So, If we treat the three bodies as a device,
Applying the law of linear momentum conservation,
\[\Rightarrow m{{v}_{0}}=2mv\prime \]
$\Rightarrow v'=\dfrac{{{v}_{0}}}{2}$
Therefore, A will be having the velocity
$\Rightarrow v'=\dfrac{{{v}_{0}}}{2}$
(b) Now, let us solve for the B part
If we consider the three bodies to be a system
Therefore, net external force = 0
Therefore, the velocity of the centre of mass will be given as:
 \[\Rightarrow {{V}_{cm}}=\dfrac{m{{v}_{0}}+2m(\dfrac{{{v}_{0}}}{2})}{m+2m}\]
\[\Rightarrow {{V}_{cm}}=\dfrac{m{{v}_{0}}+m{{v}_{0}}}{3m}\]
\[\Rightarrow {{V}_{cm}}=\dfrac{2m{{v}_{0}}}{3m}\]
\[\Rightarrow {{V}_{cm}}=\dfrac{2}{3}{{v}_{0}}\]
Therefore, the velocity of the centre of mass C of the system A+B+P will be
\[\Rightarrow {{V}_{cm}}=\dfrac{2}{3}{{v}_{0}}\]
(c) Now, for the part C
So,
The velocity of (A+P) with respect to the centre of mass will be
$\Rightarrow \dfrac{2{{v}_{0}}}{3}-\dfrac{{{v}_{0}}}{2}=\dfrac{{{v}_{0}}}{6}$
Now,
The velocity of B with respect to the centre of mass will be
\[\Rightarrow {{v}_{0}}-\dfrac{2{{v}_{0}}}{3}=\dfrac{{{v}_{0}}}{3}\] (Only considering the magnitude)
Now,
The distance of the (A+P) from centre of mass will be
$=\dfrac{1}{3}$
And that for B will be = $\dfrac{21}{3}$
So, now
By using conservation of angular momentum
We have,
\[{{P}_{cm}}={{I}_{cm}}\times \omega \]
Using the values we have
\[\Rightarrow 2m\times \dfrac{{{v}_{0}}}{6}\times \dfrac{1}{3}+m\times \dfrac{{{v}_{o}}}{3}\times \dfrac{21}{3}=2m{{(\dfrac{1}{3})}^{2}}+m{{(\dfrac{21}{3})}^{2}}\times \omega \]
\[\Rightarrow \dfrac{6m{{v}_{0}}l}{18}=\dfrac{6ml}{9}\times \omega \]
$\Rightarrow \omega =\dfrac{{{v}_{0}}}{2l}$
So, the angular speed of the system about C after the collision will be
 $\Rightarrow \omega =\dfrac{{{v}_{0}}}{2l}$

Note:
The law of conservation of momentum says in physics and chemistry that the momentum of an independent device remains constant. Therefore, momentum is said to be retained over time; that is, momentum is not produced or lost, only converted or shifted from one form to another.