Question

Two slits are made $1mm$ apart and the screen is placed one mater away. What is the fringe separation when the green light of wavelength $500nm$ is used?
$\left( A \right)500nm$
$\left( B \right)250nm$
$\left( C \right)50nm$
$\left( D \right)25nm$

Answer 1

Hint: In this problem distance between the two slits is given, wavelength of the light is also given and at the same time distance of the screen is also given. Now by using Young’s double slits formula we can calculate the separation of the fringe. So first you need to learn the double slit formula to solve this problem.
Formula Used:
$\boxed{\beta \, = \,\dfrac{{\lambda D}}{d}}$
Where,
$\beta = $ Separation of Fringe
$\lambda = $ Wavelength of Light
${\text{D = }}$ Distance of the screen
${\text{d = }}$ Distance between two slit

Complete step-by-step solution:
In modern physics the double slit’s experiment is a demonstration that light and matter can display characteristics of both classically defined waves and particles, moreover , it displays the fundamentally probabilistic nature of quantum mechanical phenomena.

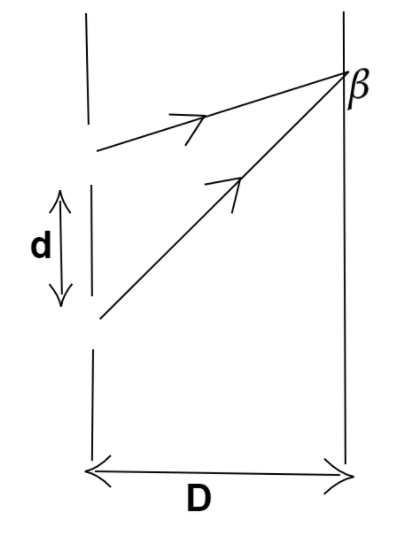
As given in the question,
There are two slits at a distance of $1mm$ from each other.
Now convert first convert the distance between the two slits into meters.
$1mm = {10^{ - 3}}m$
The screen is at a distance of $1m$ .
And the wavelength of the given green light is $500nm$ .
Now first convert the wavelength into meter we get,
$1nm = {10^{ - 9}}m$
$ \Rightarrow 500nm = 500 \times {10^{ - 9}}m$
Now using young’s double slit formula we get,
$\boxed{\beta \, = \,\dfrac{{\lambda D}}{d}}$
Putting the given values we will get,
$\beta = \dfrac{{500 \times {{10}^{ - 9}}m \times 1m}}{{{{10}^{ - 3}}m}}$
$ \Rightarrow \beta = \dfrac{{500 \times {{10}^{ - 9}}{m^2}}}{{{{10}^{ - 3}}m}}$
$ \Rightarrow \beta = 500 \times {10^{ - 6}}m$
$ \Rightarrow \beta = 5 \times {10^{ - 4}}m$
Converting meter into nanometer,
$ \Rightarrow \beta = 5 \times {10^{ - 4}} \times {10^9} \times {10^{ - 9}}m$
$ \Rightarrow \beta = 5 \times {10^5}nm$
$ \Rightarrow \boxed{\beta = 500000nm}$
Hence the fringe separation is $500000nm$.
But the correct option is not given in the question.

Note: So as to get a simplified answer, always keep all SI units in the same terms like in this question first convert all the given values in terms of the same SI unit. Always convert all the given terms into its basic SI unit. Then according to the option change the final value’s SI unit.