Question

Two sides of a rhombus are along the lines, $ x - y + 1 = 0 $ and $ 7x - y - 5 = 0. $ If its diagonals intersect at $ ( - 1, - 2), $ then which one of the following is a vertex of this rhombus?
A. $ ( - 3, - 8) $
B. $ \left( {\dfrac{1}{3},\dfrac{{ - 8}}{3}} \right) $
C. $ \left( {\dfrac{{10}}{3},\dfrac{{ - 7}}{3}} \right) $
D. $ ( - 3, - 9) $

Answer 1

Hint: Here, first of all we will draw the diagram with the help of the given specifications and then find the slope of the lines and the line equation with the slope and then place the points given in the options to check whether it satisfies the line equation or not.

Complete step-by-step answer:
Draw the diagram with the help of the given data- As we know that in Rhombus the diagonals intersect at right angles.

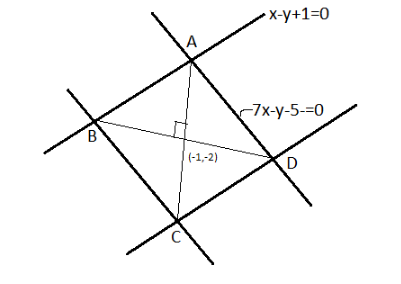
Now, take the two given lines –
  $ x - y + 1 = 0 $ .... (I)
  $ 7x - y - 5 = 0. $ ..... (II)
Now, the equation (II) minus (I)
  $ \Rightarrow 6x - 6 = 0 $
Simplify the above equation. When the term is moved from one side to another, the sign also changes. Positive terms become negative and vice versa.
  $
   \Rightarrow 6x = 6 \\
   \Rightarrow x = \dfrac{6}{6} \;
   $
Common factors from the numerator and the denominator cancel each other.
  $ \Rightarrow x = 1 $
Place the value of “x” in equation (I)
  $
   \Rightarrow x - y + 1 = 0 \\
   \Rightarrow 1 - y + 1 = 0 \;
   $
Simplify the equation –
  $ \Rightarrow y = 2 $
Therefore the coordinates of point A is $ (1,2) $
Now, the slope between the two perpendicular lines is for the co-ordinates $ (1,2)\,{\text{and ( - 1, - 2)}} $ is
  $ m = \left( {\dfrac{{2 - ( - 2)}}{{1 - ( - 1)}}} \right) $
Simplify the above equation –
  $ m = \dfrac{4}{2} $
Common multiple from the numerator and the denominator cancel each other.
  $ \Rightarrow m = 2 $
Product of slopes of two perpendicular lines is always equal to $ ( - 1) $
  $ \Rightarrow m.m' = ( - 1) $
Place the values –
  $
   \Rightarrow m'(2) = -1 \\
   \Rightarrow m' = \dfrac{-1}{2} \;
   $
Equation of line passing through $ ( - 1, - 2) $ and slope $ m' = \dfrac{1}{2} $ is
  $ \Rightarrow y + 2 = \dfrac{{ - 1}}{2}(x + 1) $
Simplify the equation –
  $ \Rightarrow 2y + 4 = - (x + 1) $
Open the brackets. Negative sign outside the bracket changes sign of all the terms inside the bracket.
  $ \Rightarrow 2y + 4 = - x - 1 $
Take all the terms on one side of the equation –
  $ \Rightarrow x + 2y + 5 = 0 $
Take the options given and place the values in the above equation
– $ (x,y) = ( - 3, - 8) $
  $
   \Rightarrow x + 2y + 5 = 0 \\
   \Rightarrow - 3 + 2( - 8) + 5 = - 3 - 16 + 5 \ne 0 \;
   $
Similarly for all the points –
  $ (x,y) = \left( {\dfrac{1}{3},\dfrac{{ - 8}}{3}} \right) $
  $
   \Rightarrow x + 2y + 5 = 0 \\
   \Rightarrow \dfrac{1}{3} + 2(\dfrac{{ - 8}}{3}) + 5 = \dfrac{{1 - 16 + 15}}{3} = 0 \;
   $
Points $ (x,y) = \left( {\dfrac{1}{3},\dfrac{{ - 8}}{3}} \right) $ satisfies the line equation
So, the correct answer is “Option B”.

Note: Always remember the properties of the slopes and the slopes of two perpendicular lines. Also, remember that the diagonals of the rhombus always intersect at right angles and the rhombus has all the four sides equal and opposite two sides of the rhombus are parallel to each other.