Question

Two sides of a parallelogram are 20 cm and 25 cm. If the altitude corresponds to the sides of length 25 cm is 10 cm. Find the altitude corresponding to the other pair of the sides.

Answer 1

Hint: Area of a parallelogram is equal to the product of the base and the height of the parallelogram. In this question length of both sides of parallelogram are given and length of their corresponding altitudes are also given so by using the area of the parallelogram formula we will equate the areas to find the missing side.

Complete step-by-step answer:
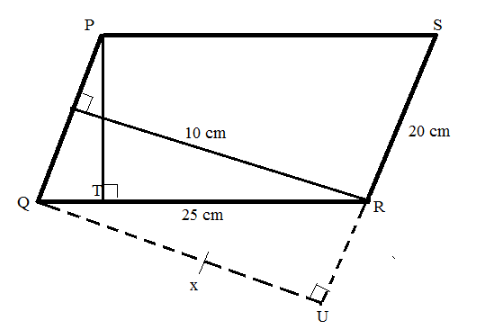
Given the two sides of the parallelogram PQRS as
PS=QR=25 cm
PQ=SR=20 cm
We know the area of a parallelogram is the product of their base and their height and for the base QR we can see PT is its altitude and for the base SR its altitude is QU, hence we can write this as
 \[QR \times PT = SR \times QU\]
Now we will substitute the values of the corresponding base and their altitude to find the length of the side QU
 \[
\Rightarrow 25 \times 10 = 20 \times QU \\
\Rightarrow QU = \dfrac{{250}}{{20}} \\
   = 12.5\;cm \\
 \]
Now since the side QU is denoted as the symbol x, hence we can the altitude corresponding to the other pair of the sides is \[x = 12.5\;cm\]
So, the correct answer is “12.5 cm”.

Note: Another method to find the area of a parallelogram is the half of the product of the length of the diagonals which are intersecting at any angle in corresponding to the sine function.
Given by the formula \[Area = \dfrac{1}{2} \times {d_1} \times {d_2}\sin \left( x \right)\] . In this question since the length of the diagonals are not given so we will find the area using base and the altitude.