Question

Two ships are there in the sea on either side of a lighthouse in such a way that the ships and the lighthouse are in the same straight line. The angles of depression of two ships observed from the top of the lighthouse are ${60^ \circ }$ and ${45^ \circ }$ respectively. If the height of the lighthouse is $200$ m, find the distance between the two ships. (Use $\sqrt 3 = 1.73$)

Answer 1

Hint: We will use trigonometric formulas to solve this question. First, we will draw the figure according to the condition and we will apply the trigonometric formulas such as $\tan {\theta ^ \circ } = \dfrac{{opposite}}{{adjacent}}$.

Complete step-by-step solution:
Let us draw a figure in which PR represents the lighthouse and QS represents the distance between two ships such that Q – R – S.
Q is the ${1^{st}}$ ship and S is the ${2^{st}}$
The height of the lighthouse is $PR = 200m$
The angle of depression for ${1^{st}}$ ship is ${60^ \circ }$ and the angle of depression for ${2^{st}}$ ship is ${45^ \circ }$

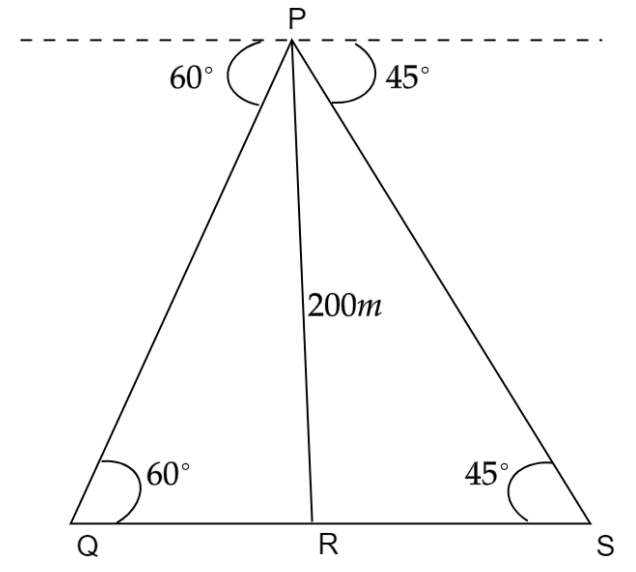
Line P and line QS are parallel.
Therefore,
$\angle PQS = {60^ \circ }$ and $\angle PSQ = {45^ \circ }$ (Alternate angles between two parallel lines are congruent)
In $\Delta PQR$,
$\tan {60^ \circ } = \dfrac{{opposite}}{{adjacent}} = \dfrac{{PR}}{{QR}}$
Substituting $\tan {60^ \circ } = \sqrt 3 $ and $PR = 200m$,
$\sqrt 3 = \dfrac{{200}}{{QR}}$
Rearranging the terms,
$QR = \dfrac{{200}}{{\sqrt 3 }}$
Putting value of $\sqrt 3 = 1.73$,
$QR = \dfrac{{200}}{{1.73}}m$
In $\Delta PRS$,
$\tan {45^ \circ } = \dfrac{{opposite}}{{adjacent}} = \dfrac{{PR}}{{RS}}$
Substituting $\tan {45^ \circ } = 1$ and $PR = 200m$,
$1 = \dfrac{{200}}{{RS}}$
Rearranging the terms,
$RS = 200m$
The ships and the lighthouse are all in a straight line such that Q – R – S.
Therefore, we can write,
$QS = QR + RS$
We know the values of QR and RS,
Substituting those values,
$QS = \dfrac{{200}}{{\sqrt 3 }} + 200$
Making the denominator same,
$QS = \dfrac{{200}}{{\sqrt 3 }} + \dfrac{{200\sqrt 3 }}{{\sqrt 3 }}$
Since the denominator is same, we can add the numerator part,
$QS = \dfrac{{200 + 200\sqrt 3 }}{{\sqrt 3 }}$
Taking $200$ common from numerator,
$QS = \dfrac{{200(1 + \sqrt 3 )}}{{\sqrt 3 }}$
Substituting the value of $\sqrt 3 = 1.73$,
$QS = \dfrac{{200(1 + 1.73)}}{{1.73}}$
Adding the terms,
$QS = \dfrac{{200(2.73)}}{{1.73}}$
Simplifying the terms,
$QS = 315.60$
Therefore, the distance between the two ships is $315.60m$.

Note: The angle of depression is the angle between a horizontal line from the observer and the line of sight to an object that is below the horizontal line. The angle of elevation is the angle between a horizontal line from the observer and the line of sight to an object that is above the horizontal line. This problem is based on solutions of triangles where we establish a relation b/w unknown values and given data with the help of different trigonometric ratios.