Question

Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse observed from the ships are \[{{30}^{0}},{{60}^{0}}\] respectively. If the lighthouse is 100 m high, find the distance between the two ships.

Answer 1

Hint: To solve the question, we have to represent the given information in the diagrammatic format to analyse the given data and to convert the problem into a geometry problem which will ease the procedure of solving. To solve further, apply the trigonometric angles formula of triangles for calculating the distance between the two ships which are on two sides of the lighthouse.

Complete step-by-step answer:
Let the two ships sailing in the sea on the two sides of the lighthouse be A, B.
Let CD be the height of the lighthouse with C at its top.
Thus, CD = 100 m.
The given angle of elevation of the top of the lighthouse from the two ships which are along the two sides of the lighthouse are \[{{30}^{0}},{{60}^{0}}\] respectively.

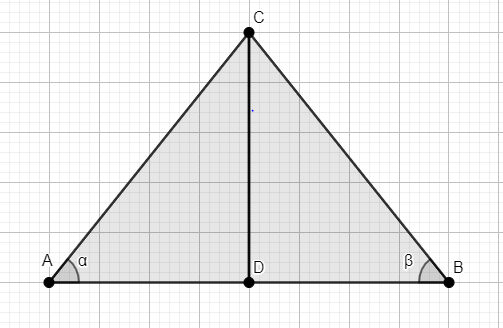
Thus, the value of \[\alpha ,\beta \] are \[{{30}^{0}},{{60}^{0}}\] respectively.
We know that the trigonometric formula for the tan of angle is equal to the ratio of the opposite side of the triangle and adjacent side of the triangle.
Consider \[\Delta ACD\]
By applying the above trigonometric formula of tan angle, we get
\[\tan \alpha =\dfrac{CD}{AD}\]
\[\tan {{30}^{0}}=\dfrac{100}{AD}\]
We know that the value of \[\tan {{30}^{0}}=\dfrac{1}{\sqrt{3}}\]
By applying the value, we get
\[\dfrac{1}{\sqrt{3}}=\dfrac{100}{AD}\]
\[\Rightarrow AD=100\sqrt{3}\] ….. (1)
Consider \[\Delta BCD\]
By applying the above trigonometric formula of tan angle, we get
\[\tan \beta =\dfrac{CD}{BD}\]
\[\tan {{60}^{0}}=\dfrac{100}{AD}\]
We know that the value of \[\tan {{60}^{0}}=\sqrt{3}\]
By applying the value, we get
\[\sqrt{3}=\dfrac{100}{BD}\]
\[\Rightarrow BD=\dfrac{100}{\sqrt{3}}\] ….. (2)
The distance between the two ships which are on two sides of the lighthouse = The sum of distances between the ships and the base
= AD + BD
By substituting the values from the equations (1) and (2) in the above equation, we get
\[\begin{align}
  & =100\sqrt{3}+\dfrac{100}{\sqrt{3}} \\
 & =\dfrac{\left( 100\sqrt{3} \right)\sqrt{3}+100}{\sqrt{3}} \\
 & =\dfrac{\left( 100{{\left( \sqrt{3} \right)}^{2}} \right)+100}{\sqrt{3}} \\
 & =\dfrac{\left( 100\times 3 \right)+100}{\sqrt{3}} \\
 & =\dfrac{300+100}{\sqrt{3}} \\
 & =\dfrac{400}{\sqrt{3}} \\
\end{align}\]
Thus, the distance between the two ships which are on two sides of the lighthouse is equal to \[\dfrac{400}{\sqrt{3}}m\]
Note: The possibility of mistake can be, not able to represent the given information in the diagrammatic format which will ease the analysis of the given question. The other possibility of mistake can be not applying the trigonometric angles formula for calculating the answer.