Question

Two ships are sailing in the sea on either side of the lighthouse; the angle of depression of two ships as observed from the top of the lighthouse are ${{60}^{\circ }}$ and ${{45}^{\circ }}$ respectively. If the distance between the ships is $200\left( \dfrac{\sqrt{3}+1}{\sqrt{3}} \right)$ meters, find the height of the lighthouse.

Answer 1

Hint: Assume the distance between the base of the lighthouse and ship 1 be $x$ and that between the ship 2 and base of the lighthouse be $y$. Height of the tower can be considered as $h$. Use tangent of the given angles to find the value of $h$.

Complete Step-by-step answer:
The term angle of depression denotes the angle from the horizontal downward to an object an observer’s line of sight would be below the horizontal.
Now, let us come to the question. Let us assume that AM is the tower and ship 1 is at B and ship 2 is at C. Here, we have assumed $BM=x$ and $CM=y$. Also, $\angle ABM={{60}^{\circ }}$ and $\angle ACM={{45}^{\circ }}$, as they are alternate angles with their respective angle of depression. We know that, $\tan \theta =\dfrac{perpendicular}{\text{base}}$.

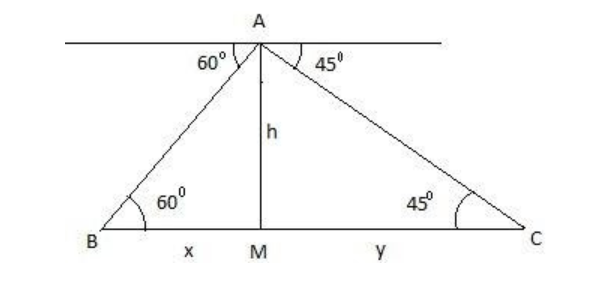
In triangle AMC,
$\begin{align}
  & \tan {{45}^{\circ }}=\dfrac{h}{y} \\
 & 1=\dfrac{h}{y} \\
 & y=h............................(i) \\
\end{align}$

In triangle AMB,
$\begin{align}
  & \tan {{60}^{\circ }}=\dfrac{h}{x} \\
 & \sqrt{3}=\dfrac{h}{x} \\
 & x=\dfrac{h}{\sqrt{3}}........................(ii) \\
\end{align}$
Now, it is given that the distance between the ships is $200\left( \dfrac{\sqrt{3}+1}{\sqrt{3}} \right)$ m. Therefore,
$\begin{align}
  & x+y=200\left( \dfrac{\sqrt{3}+1}{\sqrt{3}} \right) \\
 & \dfrac{h}{\sqrt{3}}+h=200\left( \dfrac{\sqrt{3}+1}{\sqrt{3}} \right) \\
 & h\left( \dfrac{\sqrt{3}+1}{\sqrt{3}} \right)=200\left( \dfrac{\sqrt{3}+1}{\sqrt{3}} \right) \\
 & h=200\text{ m} \\
\end{align}$
Hence, the height of the tower is 200 m.

Note:It is important to draw the diagram of the situation, so that it can be easy to understand what we are going to find out. Also, here tangent of the angle is used to solve the question because we have been provided with the base of the triangle and the value of perpendicular is required.