Question

Two ships are 10km apart on a line from south to north. The one farther north is moving towards the west at 40kmph and the other is moving towards the north at 40kmph. The distance of their closest approach is
A. $10km$
B. $10\sqrt{2}km$
C.$\dfrac{10}{\sqrt{2}}km$
D. $20km$

Answer 1

Hint: As a first step, you could depict the whole situation in a diagram. Then you could find the direction of the resultant of the two velocities of the ships A and B. Then you could assume one of the ships is at rest and the other is moving with the resultant velocity and thus find the distance of closest approach.
Formula used:
Relative velocity,
${{V}_{AB}}={{V}_{A}}-{{V}_{B}}$

Complete answer:
In the question, we are given two ships that are 10km apart from each other and are kept on a line from south to north. Both are moving with the same velocity 40kmph but in different directions. One is headed towards west while other towards north. We are asked to find the distance of closest approach using the given information.
Firstly, let us depict the given situation in a diagram.

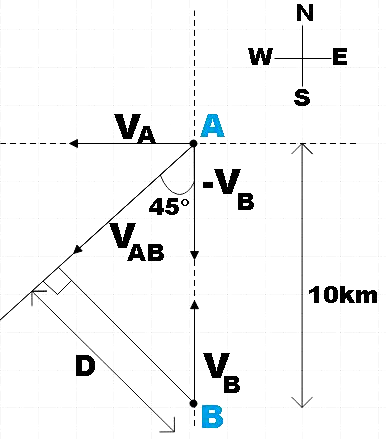
Let the ships be at positions A and B that are 10km apart initially as shown. Now, ship A is moving towards west and ship B is headed due north with the same speed. Then we could find the resultant velocity of the two ships as,
${{V}_{AB}}={{V}_{A}}-{{V}_{B}}$
As both velocities are of equal magnitude, the angle made by these vectors with the resultant will be $45{}^\circ $ and the resultant will be directed in the south-west direction as shown.
Now we assume that the ship B is at rest and it is just ship$A$ moving with the velocity ${{V}_{AB}}$. So, we could draw perpendicular from ship B at rest to the path the ship A is assumed to take. This is the distance of closest approach D.
From the figure, we see that,
$\sin 45{}^\circ =\dfrac{D}{AB}$
$\Rightarrow D=AB\times \sin 45{}^\circ =10\times \dfrac{1}{\sqrt{2}}$
$\therefore D=\dfrac{10}{\sqrt{2}}km$
Therefore, we found the distance of closest approach of the given ships to be $\dfrac{10}{\sqrt{2}}km$.

Hence, option C is found to be the correct answer.

Note:
It is not necessary to find the value of the relative of the velocities of the ships. But if we were asked to find it we could easily find it by assigning the correct as per the given directions. So,
${{V}_{A}}=-40kmph$
${{V}_{B}}=40kmph$
$\Rightarrow {{V}_{AB}}={{V}_{A}}-{{V}_{B}}=-40-40$
$\therefore {{V}_{AB}}=-80kmph$
So, the relative velocity of the ships will be -80kmph.