Question

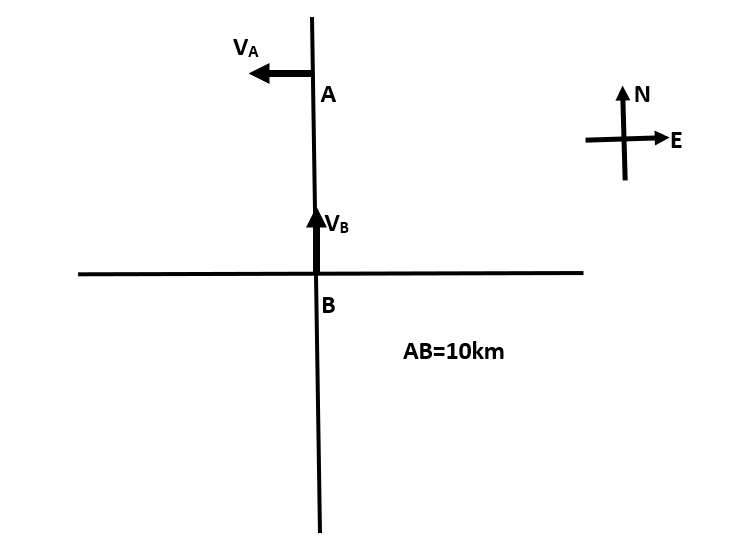
Two ships A and B are 10km apart on a line running South to North. Ship A which is farther North is streaming West at $20kmh{{r}^{-1}}$ and Ship B is streaming North at $20kmh{{r}^{-1}}$ . What is their distance of closest approach and how long do they take to reach it?
 

Answer 1

Hint: To find the distance of closest approach, we first calculate the relative velocity of one ship with respect to another. This makes one of the ships stationary, so it's easy to move ahead now. Now, from the stationary shop we drop a perpendicular on the line of direction of the moving ship. This perpendicular distance is the minimum distance of approach of the two ships.

Complete answer:
Let us calculate the velocity of ship B with respect to ship A. Then, we have to subtract the velocity of ship A from ship B, as it will relatively at rest with respect to B. Let us understand this by the following figure:

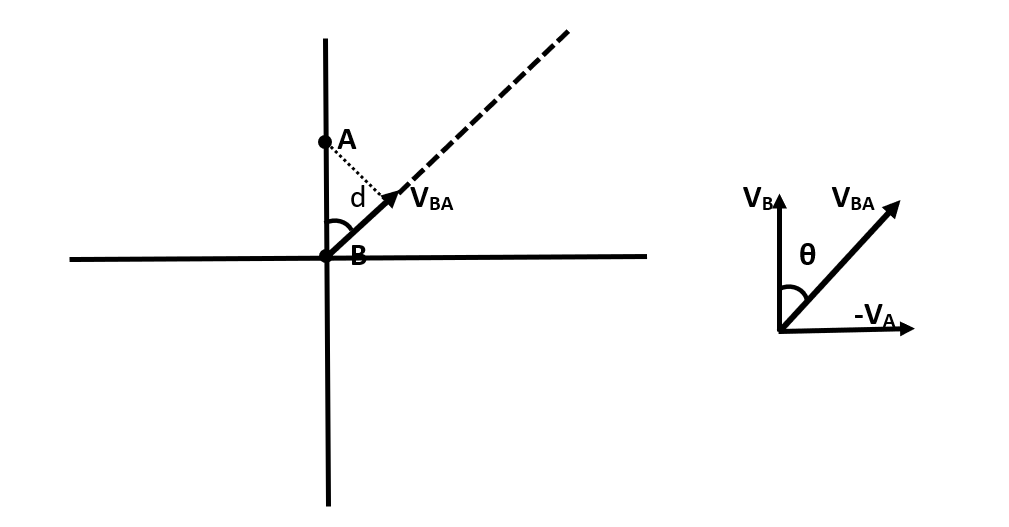
Here, we see the resultant vector $\overrightarrow{{{V}_{BA}}}$ making an angle $\theta $ with vector $\overrightarrow{{{V}_{B}}}$ which is also the angle made by vector $\overrightarrow{{{V}_{BA}}}$ with the line joining AB.
Now, since both the vectors are equal in magnitude, therefore the value of angle $\theta $ is equal to
$={{45}^{0}}$
Also, the magnitude of vector $\overrightarrow{{{V}_{BA}}}$ is equal to:
$\begin{align}
  & \Rightarrow \left| {{V}_{BA}} \right|=\sqrt{{{\left( 20 \right)}^{2}}+{{(20)}^{2}}}kmh{{r}^{-1}} \\
 & \Rightarrow \left| {{V}_{BA}} \right|=20\sqrt{2}kmh{{r}^{-1}} \\
\end{align}$
Now, it has been given in the problem that,
$\Rightarrow AB=10km$
Therefore, the distance of closest approach (say d) will be equal to:
$\begin{align}
  & \Rightarrow d=AB\cos {{45}^{0}} \\
 & \Rightarrow d=10\times \dfrac{1}{\sqrt{2}} \\
 & \Rightarrow d=5\sqrt{2}km \\
\end{align}$
Now, let the time taken for traversing this distance be (t) hours. Then, (t) can be calculated using the distance formula as follows:
$\begin{align}
  & \Rightarrow d=\left| {{V}_{BA}} \right|\times t \\
 & \Rightarrow t=\dfrac{d}{\left| {{V}_{BA}} \right|} \\
\end{align}$
Putting the values of all the known terms in the above equation, we get:
$\begin{align}
  & \Rightarrow t=\dfrac{5\sqrt{2}}{20\sqrt{2}}hr \\
 & \Rightarrow t=\dfrac{1}{4}hr \\
 & \Rightarrow t=\left( \dfrac{1}{4}\times 60 \right)\min \\
 & \Rightarrow t=15\min \\
\end{align}$
Hence, the distance of closest approach comes out to be $5\sqrt{2}km$ and the time taken to traverse this distance comes out to be 15 minutes.

Note:
In this problem, if we had used both the velocities in our calculations, then our solution would be larger and calculations would have become more cumbersome. So, it is important to know the approach of different types of questions under different circumstances. It helps us save time and effort and also reduces the chances of error.