Question

Two semi-circular rings of linear mass densities \[\lambda \] and \[2\lambda \], and of radius ‘\[R\]’ each are joined to form a complete ring. The distance of the centre of the mass of complete ring from its geometrical centre is:
A.\[\dfrac{{3R}}{{8\pi }}\]
B.\[\dfrac{{2R}}{{3\pi }}\]
C.\[\dfrac{{3R}}{{4\pi }}\]
D.None of these

Answer 1

Hint: First we know a circular ring is a plane figure bounded by the circumference of two concentric circles of two different radii. Here we have to take two semi-circular rings one below the other. First find the mass of the two rings. After that, finding the distance of the centre of the masses of two rings to its centre means origin. Using the formula of finding the distance of the centre of a complete ring from its geometrical centre when two semi-circular rings are given.

Complete step by step solution:

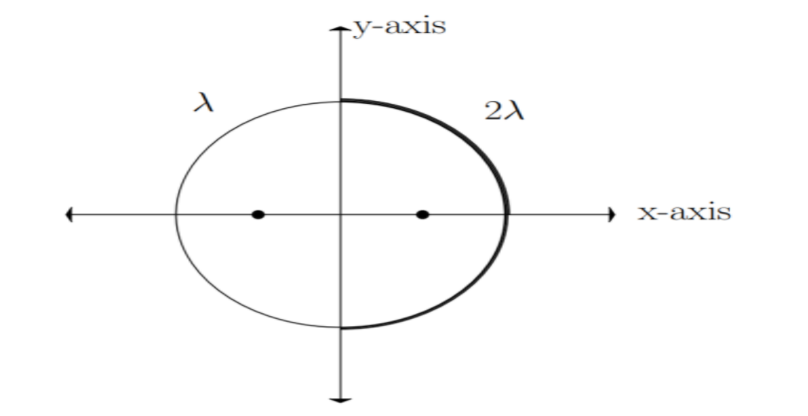
In this figure the first semi-circular ring lies in the negative x-axis and the second semi-circular ring lies in the positive x-axis. Given linear mass densities \[\lambda \]and \[2\lambda \] of two semi-circular rings and a radius \[R\]. Let \[{m_1}\] and \[{m_2}\] be the masses of first and second semi-circular rings respectively. Let \[{r_1}\] and \[{r_2}\] be the distances of mass of the first and second rings from its origin.
Since we know that \[density = \dfrac{{mass}}{{volume}}\] and volume occupy by each semicircle when radius \[R\] is \[\pi R\]. Then we get \[{m_1} = \lambda \pi R\] and \[{m_2} = 2\lambda \pi R\] .
We know that the centre of mass of a semi-circular ring is \[\dfrac{{2R}}{\pi }\].
Since each is joined to form a complete ring. Consider the two semi-circular rings in positive y-axis direction. We can form a complete ring only if one is below the other, after forming let the centre of the complete ring be \[\left( {0,0,} \right)\].
so, the centre of mass of the first semi-circular ring is \[\left( {0, - \dfrac{{2R}}{\pi }} \right)\].
Similarly, the centre of mass of the second semi-circular ring is \[\left( {0,\dfrac{{2R}}{\pi }} \right)\].
Hence \[{r_1} = - \dfrac{{2R}}{\pi }\] and \[{r_2} = \dfrac{{2R}}{\pi }\].
The distance of the centre from its geometrical centre \[ = \dfrac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}} = \dfrac{{\left( {\lambda \pi R} \right)\left( { - \dfrac{{2R}}{\pi }} \right) + 2\lambda \pi R\left( {\dfrac{{2R}}{\pi }} \right)}}{{\left( {\lambda \pi R} \right) + \left( {2\lambda \pi R} \right)}} = \dfrac{{2R}}{{3\pi }}\].
Hence Option (B) is correct.
So, the correct answer is “Option B”.

Note: Note that the centre of mass is a position defined relative to an object or system of objects. Sometimes the centre of mass doesn't fall anywhere on the object. For example, the centre of mass of a ring is located at its origin, where there isn't any material.