Question

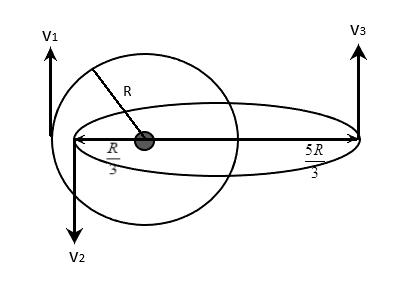
Two satellites revolve around the sun as shown in the figure. First satellite revolves in a circular orbit radius $ R $ with speed $ {v_1} $. Second satellite revolves in an elliptical orbit, for which the minimum and maximum distance from the sun are $ \dfrac{R}{3} $ and $ \dfrac{{5R}}{3} $ respectively. Velocities at these positions are $ {v_2} $ and $ {v_3} $ respectively. The correct order of speeds is

Answer 1

Hint: The kinetic energy of a satellite in orbit around the sun is inversely proportional to the distance from the sun. The kinetic energy is directly proportional to the square of the velocity.

Formula used: In this solution we will be using the following formulae;
 $ KE = \dfrac{{GMm}}{{2R}} $ where $ KE $ is the kinetic energy of a satellite in orbit, $ G $ is the universal gravitational constant, $ M $ is the mass of the orbited body (like the sun), $ m $ is the mass of the satellite, and $ R $ is the distance of the satellite from the orbited body.
 $ KE = \dfrac{1}{2}m{v^2} $ where $ KE $ is the kinetic energy of any object in motion, $ m $ is the mass of such an object, and $ v $ is the velocity.

Complete Step-by-Step solution:
We see two trajectories of two different satellites orbiting the sun. we are to find the order of the three speeds. One is the speed of the circular satellite, and two are the speeds of the elliptical satellite at the nearest point and at the farthest point from the sun.
Generally, the instantaneous kinetic energy of a given satellite can be given as
 $ KE = \dfrac{{GMm}}{{2R}} $ where $ KE $ is the kinetic energy of a satellite in orbit, $ G $ is the universal gravitational constant, $ M $ is the mass of the orbited body (like the sun), $ m $ is the mass of the satellite, and $ R $ is the distance of the satellite from the orbited body.
Hence, for the circular orbit with a radius $ R $ , the kinetic energy is
 $ K{E_1} = \dfrac{{GMm}}{{2R}} $
But, $ KE = \dfrac{1}{2}m{v^2} $ where $ KE $ is the kinetic energy of any object in motion, $ m $ is the mass of such object, and $ v $ is the velocity.
Hence,
 $ \dfrac{1}{2}m{v_1}^2 = \dfrac{{GMm}}{{2R}} $
 $ \Rightarrow {v_1} = \sqrt {\dfrac{{GM}}{R}} $
Similarly for the second satellite at radius $ \dfrac{R}{3} $ ,
 $ {v_2} = \sqrt {\dfrac{{3GM}}{R}} $
And finally at the farthest distance $ \dfrac{{5R}}{3} $
 $ {v_3} = \sqrt {\dfrac{{3GM}}{{5R}}} $
Hence, we see that $ {v_2} > {v_1} > {v_3} $ .

Note:
Alternatively, for examination purpose, we may simply note that the velocity is inversely proportional to the square root of the distance from the sun. Then since
 $ \dfrac{{5R}}{3} > R > \dfrac{R}{2} $ then
 $ {v_3} < {v_1} < {v_2} $ or $ {v_2} > {v_1} > {v_3} $ .