
Two positive charges $+q$ each are fixed at points $\left( -a,0 \right)$ and $\left( a,0 \right)$. A third charge $+Q$ is placed at the origin. Corresponding to the small displacement in the direction mentioned in the column $1$. Match the corresponding equilibrium of the column $2$.
List 1 List 2 A. Along the positive x-axis 1. stable equilibrium B. Along the positive y-axis 2. unstable equilibrium C. Along the positive z-axis 3. neutral equilibrium D. Along the line $x=y$ 4. no equilibrium
A. $A\to 1,B\to 2,C\to 2,D\to 4$
B. $B\to 1,C\to 2,D\to 2,A\to 4$
C. $C\to 1,D\to 2,A\to 2,B\to 4$
D. $D\to 1,A\to 2,B\to 2,C\to 4$
| List 1 | List 2 |
| A. Along the positive x-axis | 1. stable equilibrium |
| B. Along the positive y-axis | 2. unstable equilibrium |
| C. Along the positive z-axis | 3. neutral equilibrium |
| D. Along the line $x=y$ | 4. no equilibrium |
Answer
574.5k+ views
Hint: In the equilibrium condition the torque and the force acting on the system should be zero. So, if the potential energy of the system is high. The system is unstable and the system will be stable for the minimum potential energy.
Complete answer:
As per the condition mentioned in the question, the arrangement of the charges can be visualized as the following diagram,
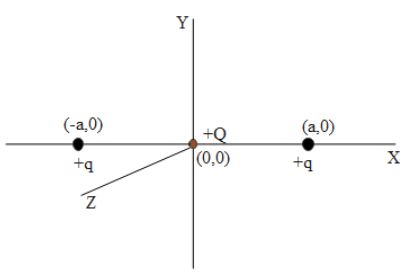
The force induced on the dipole (dipole is of two positive charges ($+q,+q$) ) to rotate around the axis due to an external charge $\left( +Q \right)$ is known as toques. The torque is a cross product of the electric dipole moment and the electric field.
Mathematically,
$\begin{align}
& \vec{\tau }=\vec{p}\times \vec{E} \\
& \Rightarrow \vec{\tau }=\left| p \right|\left| E \right|\sin \theta \\
\end{align}$
For equilibrium, the value of torques should be zero,
$\begin{align}
& pE\sin \theta =0 \\
& \Rightarrow \sin \theta =0 \\
& \Rightarrow \theta =0\,or\,\pm \pi \\
\end{align}$
So the system will be in equilibrium only when the change in the angle due to displacement of the charge remains zero.
So the system will be stable only in displacement along the x-axis.
When the charge $+Q$ is displaced such that the distance of charge along the x-axis is equivalent to the y-axis $\left( x=y \right)$.
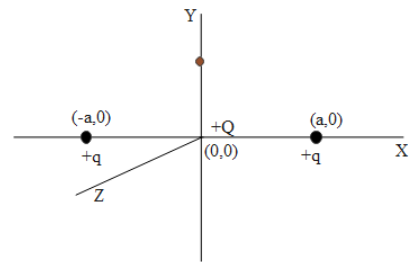
There will be no equilibrium.
Thus, by referring to the list 1 and 2 in the question the correct option to satisfy the question is Option A.
Note:
The stability of a setup where the dipole is affected by some external charge or field can also be studied through potential energy formed in the setup. The potential energy is maximum when the phase angle between the dipole moment and the electric field is $180{}^\circ $. At this point, the system will be highly unstable. At the phase angle, $\theta =0$ the system will have the least potential energy and it will be in equilibrium.
Complete answer:
As per the condition mentioned in the question, the arrangement of the charges can be visualized as the following diagram,

The force induced on the dipole (dipole is of two positive charges ($+q,+q$) ) to rotate around the axis due to an external charge $\left( +Q \right)$ is known as toques. The torque is a cross product of the electric dipole moment and the electric field.
Mathematically,
$\begin{align}
& \vec{\tau }=\vec{p}\times \vec{E} \\
& \Rightarrow \vec{\tau }=\left| p \right|\left| E \right|\sin \theta \\
\end{align}$
For equilibrium, the value of torques should be zero,
$\begin{align}
& pE\sin \theta =0 \\
& \Rightarrow \sin \theta =0 \\
& \Rightarrow \theta =0\,or\,\pm \pi \\
\end{align}$
So the system will be in equilibrium only when the change in the angle due to displacement of the charge remains zero.
So the system will be stable only in displacement along the x-axis.
When the charge $+Q$ is displaced such that the distance of charge along the x-axis is equivalent to the y-axis $\left( x=y \right)$.

There will be no equilibrium.
Thus, by referring to the list 1 and 2 in the question the correct option to satisfy the question is Option A.
Note:
The stability of a setup where the dipole is affected by some external charge or field can also be studied through potential energy formed in the setup. The potential energy is maximum when the phase angle between the dipole moment and the electric field is $180{}^\circ $. At this point, the system will be highly unstable. At the phase angle, $\theta =0$ the system will have the least potential energy and it will be in equilibrium.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




