Question

Two poles standing on a horizontal ground are of heights 5 m and 10 m respectively. The line joining their tops makes an angle of ${{15}^{\circ }}$ with the ground. Then the distance ( in m) between the poles is, :
A. $\dfrac{5}{2}\left( 2+\sqrt{3} \right)$
B. $5\left( \sqrt{3}+1 \right)$
C. $5\left( 2+\sqrt{3} \right)$
D. $10\left( \sqrt{3}-1 \right)$

Answer 1

Hint: We will first draw the figure according to the conditions given in the question. We will then assume the distance between the poles as x. In the figure we will get a right angled triangle so we will use the trigonometric ratios to get the value of x.

Complete step-by-step answer:
We have been given the question that there are 2 poles of heights 5 m and 10 m respectively and the line joining their tops makes an angle of ${{15}^{\circ }}$ with the ground. To solve the question, we will consider a relative diagram as below.

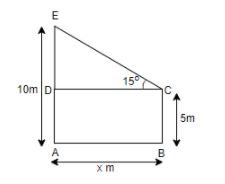
Let us assume x as the distance between the two poles. We can see that ABCD is a rectangle where, AB = x and DC = x and AD = BC = 5 m. Since AD is the second pole of 10 m, and AD = 5 m, we will get that DE = 10 - 5 = 5 m. SO, now we get a triangle DCE, which is a right angled triangle. Now, we can use the trigonometric ratios as we have an angle and one side available with us. As we can see that DC = x, so it is the base of the triangle, and DE = 5 m, which is the perpendicular and the angle is ${{15}^{\circ }}$. SO, we will use that trigonometric ratio that involves base, perpendicular and angle, that is the tan ratio as we know that $\tan \theta =\dfrac{p}{b}$. So, we have,
$\begin{align}
  & \tan {{15}^{\circ }}=\dfrac{DE}{DC} \\
 & \Rightarrow \tan {{15}^{\circ }}=\dfrac{5}{DC} \\
\end{align}$
We know that the value of $\tan {{15}^{\circ }}=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}$, so we will substitute this value in the above equality. So, we will get,
$\begin{align}
  & \dfrac{\sqrt{3}-1}{\sqrt{3}+1}=\dfrac{5}{DC} \\
 & \Rightarrow DC\left( \sqrt{3}-1 \right)=5\left( \sqrt{3}+1 \right) \\
 & \Rightarrow DC=\dfrac{5\left( \sqrt{3}+1 \right)}{\sqrt{3}-1} \\
\end{align}$
We will now rationalise to get simplify further. So, we get,
$\begin{align}
  & DC=\dfrac{5\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}-1 \right)}\times \dfrac{\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}+1 \right)} \\
 & \Rightarrow DC=\dfrac{5{{\left( \sqrt{3}+1 \right)}^{2}}}{{{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}}} \\
 & \Rightarrow DC=\dfrac{5\left( 3+1+2\sqrt{3} \right)}{3-1} \\
 & \Rightarrow DC=\dfrac{5\left( 4+2\sqrt{3} \right)}{2} \\
 & \Rightarrow DC=\dfrac{5\times 2\left( 2+\sqrt{3} \right)}{2} \\
 & \Rightarrow DC=5\left( 2+\sqrt{3} \right)m \\
\end{align}$
So, we get the distance between the poles as $5\left( 2+\sqrt{3} \right)m$.

So, the correct answer is “Option C”.

Note: In this the distance between the poles on the ground is taken as AB, but we try to shift the reference line to DC and make it as the ground line and solve the question using the concept of trigonometric ratios. Also, as the distance or length cannot be negative, there is no barrier of quadrant.