Question

Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their feet is 12 m, the distance between their tops is
(a) 12 m
(b) 14 m
(c) 13 m
(d) 11 m

Answer 1

Hint: We will draw a figure to get a rough idea of the positions of the pole. We will be able to see a right-angled triangle in the figure. We have the lengths of the sides of this triangle. We will be able to use the Pythagoras theorem to find the distance between the tops of the two poles.

Complete step-by-step solution:
First, we will sketch a rough figure to understand the positions of the two poles.

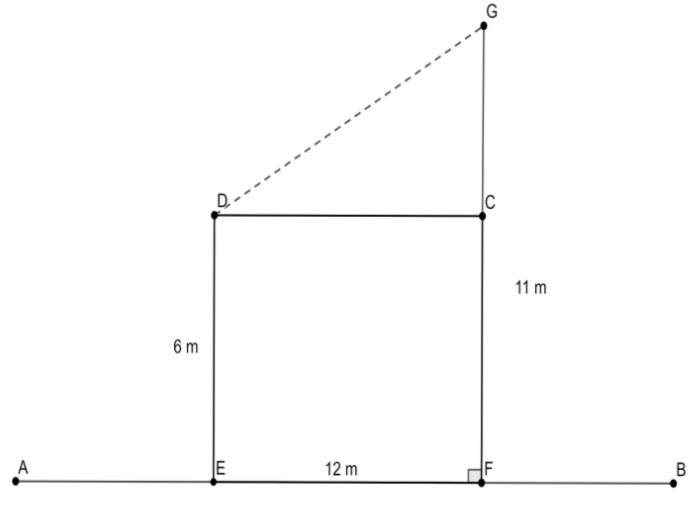
In this figure, the lengths are not to scale but we can analyze the problem. We have two poles, DE and GF with lengths 6 m and 11 m, respectively. AB is the ground. The distance between the poles is EF which is 12 m. Now, we have to find the distance between the tops of the poles, which is DG.
The poles are vertically upright. Hence, the poles make the right angle with the ground. From the figure, it can be seen that DC is parallel to EF. So we have $DC=12$m and considering GF as a transversal, $\angle CFE=\angle GCD=90{}^\circ $. Also, because $DE=CF$, we have $GC=GF-CF=11-6=5$ m. Now, we can apply the Pythagoras theorem in $\Delta GCD$. The Pythagoras theorem states that, in a right-angled triangle, ${{(Hypotenuse)}^{2}}={{(Base)}^{2}}+{{(Height)}^{2}}$.
So, we have $G{{D}^{2}}=D{{C}^{2}}+G{{C}^{2}}$. Substituting the values of DC and GC, we get the following,
\[\begin{align}
  & G{{D}^{2}}={{(12)}^{2}}+{{(5)}^{2}} \\
 & =144+25 \\
 & =169
\end{align}\]
Therefore, $GD=13$m. So, the distance between the tops of the poles is 13 m.
The correct option is (c).

Note: In this question, the figure helps us in understanding the question. Looking at the image makes it easier to find the right-angled triangle. So we can use the Pythagoras theorem and obtain the desired answer. The properties of angles made by a transversal along two parallel lines are useful in such questions.