Question

Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are \[60^\circ \] and \[30^\circ \] respectively. Find the height of the poles and the distances of the point from the poles.

Answer 1

Hint:
Here, we need to find the height of the poles and the distances of the point from the poles. We will assume the height of the poles to be \[x\] m. We will find the tangents of the given angles of elevation in the two triangles to get two equations in terms of \[x\]. We will solve these two equations using substitution to get the distances between the point and the poles, and the height of the poles.
Formula Used: The tangent in a right-angled triangle is given by \[\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}\].

Complete step by step solution:
Let the height of the equal poles be \[x\] m.
Let the distance between the first pole and the point on the road be \[y\] m.
First, we will draw the diagram for this question.

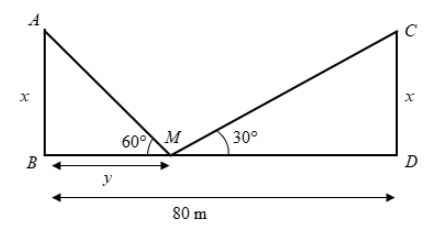
Here, \[AB\] and \[CD\] are the two poles of equal height \[x\] m. Point \[M\] is the given point on the road. The width of the road \[BD\] is 80 m. The distance between the pole \[AB\] and the point \[M\] on the road is \[y\] m.
From the diagram, we can observe that \[BM + MD = BD\].
Substituting \[BM = y\] and \[BD = 80\], we get
\[\begin{array}{l} \Rightarrow y + MD = 80\\ \Rightarrow MD = 80 - y\end{array}\]
Now, we will find the tangents in the two triangles.
We know that the tangent of an angle in a right angled triangle is given by \[\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}\].
In triangle \[ABM\], we get the tangent as
\[\tan \angle AMB = \dfrac{{AB}}{{BM}}\]
Substituting \[\angle AMB = 60^\circ \], \[AB = x\], and \[BM = y\], we get
\[ \Rightarrow \tan 60^\circ = \dfrac{x}{y}\]
Substituting \[\tan 60^\circ = \sqrt 3 \] in the equation, we get
\[ \Rightarrow \sqrt 3 = \dfrac{x}{y}\]
Multiplying both sides by \[y\], we get
\[ \Rightarrow x = \sqrt 3 y\]
Now, we will find the tangent in the triangle \[CDM\].
In triangle \[CDM\], we get the tangent as
\[\tan \angle CMD = \dfrac{{CD}}{{MD}}\]
Substituting \[\angle CMD = 30^\circ \], \[CD = x\], and \[MD = 80 - y\], we get
\[ \Rightarrow \tan 30^\circ = \dfrac{x}{{80 - y}}\]
Substituting \[\tan 60^\circ = \sqrt 3 \] and \[x = \sqrt 3 y\] in the equation, we get
\[ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{\sqrt 3 y}}{{80 - y}}\]
Simplifying the equation, we get
\[\begin{array}{l} \Rightarrow 80 - y = \sqrt 3 \times \sqrt 3 y\\ \Rightarrow 80 - y = 3y\end{array}\]
Adding \[y\] to both sides, we get
\[\begin{array}{l} \Rightarrow 80 - y + y = 3y + y\\ \Rightarrow 80 = 4y\end{array}\]
Dividing both sides by 4, we get
\[y = 20{\text{ m}}\]
Therefore, the distance between pole \[AB\] and the point \[M\] is 20 m.
Substituting \[y = 20{\text{ m}}\] in the equation \[MD = 80 - y\], we get
\[\begin{array}{l} \Rightarrow MD = 80 - 20\\ \Rightarrow MD = 60{\text{ m}}\end{array}\]
Therefore, the distance between pole \[CD\] and the point \[M\] is 60 m.
Finally, substitute \[y = 20{\text{ m}}\] in the equation \[x = \sqrt 3 y\], we get
\[\begin{array}{l} \Rightarrow x = \sqrt 3 \times 20\\ \Rightarrow x = 20\sqrt 3 {\text{ m}}\end{array}\]

\[\therefore\] The height of the poles is \[20\sqrt 3 {\text{ m}}\].

Note:
It is important for us to remember the value of trigonometric ratios for standard angles. A common mistake is to substitute \[\tan 30^\circ = \sqrt 3 \] and \[\tan 60^\circ = \dfrac{1}{{\sqrt 3 }}\]. This will give us the wrong answer.