Question

Two point charges $2\mu C$ and $8\mu C$ repel each other with force $F$ . Find how much charge should be transferred from $2\mu C$ to $8\mu C$ so that force becomes $\dfrac{F}{2}$ ?

Answer 1

Hint: In order to solve this question we must know the coulomb's law which states that the electrostatic force acts between two static point electric charges will be directly proportional to product of the charges and inversely proportional to the square of distance between them. So we will first use the formula when force is F and again when force is $\dfrac{F}{2}$ , and taking the ratio of both the equations we will get our final answer.

Formula Used:
$F=\dfrac{k{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$
where $F$ is electrostatic force, ${{q}_{1}}$ and ${{q}_{2}}$ are static point charges, $k$ is coulomb’s constant and $r$ is distance between two static point charges.

Complete step by step answer:
In our question we are given with two static point charges which are ${{q}_{1}}=2\mu C$ and ${{q}_{2}}=8\mu C$ , and the electrostatic force acting between them is $F$. While in the second case it is given that some amount of charge gets transferred from $2\mu C$ to $8\mu C$ due to this the electrostatic force between them becomes $\dfrac{F}{2}$.Note that distance between both the static point charge is $r$ in both the cases.

So from this we are asked to find what amount of charge is transferred from $2\mu C$ to $8\mu C$ and let consider that charge as $x\mu C$.

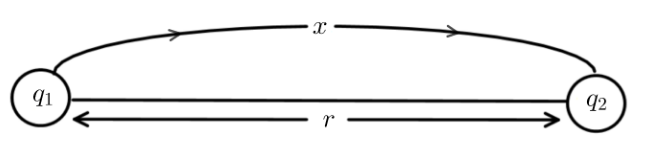
So as we discussed earlier according to coulomb's law the electrostatic force between the two point charge is given by,
$F=\dfrac{k{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$ ………………………… $\left( 1 \right)$
Now using equation $\left( 1 \right)$ in our first case when force is $F$ and ${{q}_{1}}=2\mu C$ and ${{q}_{2}}=8\mu C$ ,
$F=\dfrac{k\left( 8 \right)\left( 2 \right)}{{{r}^{2}}}$ ……………………. $\left( 2 \right)$
Now again using equation $\left( 1 \right)$ for second case where force becomes $\dfrac{F}{2}$ and as we know $x$ amount of charge transferred from $2\mu C$ to $8\mu C$ so here ${{q}_{1}}=(2-x)\mu C$ and ${{q}_{2}}=(8+x)\mu C$ so our equation will become,
$\dfrac{F}{2}=\dfrac{k\left( 8+x \right)\left( 2-x \right)}{{{r}^{2}}}$ …………………… $\left( 3 \right)$

Now taking ratio of equation $\left( 2 \right)$ and $\left( 3 \right)$ we will get,
$\dfrac{F}{F}\times 2=\dfrac{k\left( 8 \right)\left( 2 \right)}{{{r}^{2}}}\times \dfrac{{{r}^{2}}}{k\left( 8+x \right)\left( 2-x \right)}$
$\Rightarrow 2=\dfrac{\left( 8 \right)\left( 2 \right)}{\left( 8+x \right)\left( 2-x \right)}$
Cross-multiplying the denominator,
$16-6x-{{x}^{2}}=8$
$\Rightarrow {{x}^{2}}+6x-8=0$
Now, to solve the equation we can compare the above equation with the quadratic equation $a{{x}^{2}}+bx+c=0$ and we get $a=1,b=6,c=-8$

Now by further solving above equation by quadratic formula and substituting the values,
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}=\dfrac{-6\pm \sqrt{{{6}^{2}}-4\times 1\times (-8)}}{2\times 1}$
$\Rightarrow x=\dfrac{-6\pm \sqrt{68}}{2}$
$\Rightarrow x=\dfrac{-6\pm 8.24}{2}$ , from this equation we get two value of $x$,
$\therefore x=1.12$ or $x=-7.12$
Now if we place $x=-7.12$ in ${{q}_{1}}=(2-x)\mu C$ then it will not satisfy our condition because as given in our question charge from ${{q}_{1}}$ get transferred so its value must be less than $2\mu C$ but here it increases. So from this we can conclude our final answer is $x=1.12$. So from all our calculations we will conclude that $x$ amount of charge which transfer from $2\mu C$ to $8\mu C$ due to which force between them reduced to $\dfrac{F}{2}$ is $1.12\mu C$.

Note: While solving such type of questions one must remember that if both the static charge is of same sign then repulsive force will act between them but if both the charges are of opposite sign then the force act between them will be attractive, where one point to understand the formula to find the value of electrostatic force will remain same in both cases.