Question

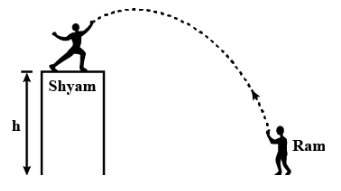
Two persons Ram and Shyam wish to throw a ball at each other as shown in the figure. The maximum horizontal distance from the building where Ram can stand and still throw a ball at Shyam is ${{d}_{1}}$. The maximum horizontal distance of Ram from the building where Shyam can throw a ball at Ram is ${{d}_{2}}$. If both of them can throw the ball with a velocity of $\sqrt{2gk}$, find $\dfrac{{{d}_{1}}}{{{d}_{2}}}$. Neglect the height of each person.

A. $\sqrt{\dfrac{k+h}{k-h}}$
B. $\sqrt{\dfrac{k-h}{k+h}}$
C. $2\sqrt{\dfrac{k+h}{k-h}}$
D. $2\sqrt{\dfrac{k-h}{k+h}}$

Answer 1

Hint:In order to solve this kind of question, we will be using the concept of kinematics. We will discuss the projectile of an object in a two dimensional plane.

Formula used:
The third equation of motion $2as={{v}^{2}}-{{u}^{2}}$
Where $u$ is the initial velocity, $s$ is the distance covered, $a$ is the acceleration and $t$ is the time taken.

Complete step by step answer:
In order to solve this question, we will be dividing our solution into two parts and then we will combine the results to find the correct answer. We need to find the equations of the maximum horizontal distances travelled by both the projections (range) and then find the ratio of them.

PART 1: (projection from the top of the building)
First of all, we will be writing the data given to us. The velocity with which the ball is projected from the top of the building $u=\sqrt{2gk}$. The distance covered by the ball projected by Shyam from the top of the building $s=h$. The acceleration due to gravity$a=g$. Here the acceleration is positive because the direction of the ball is downwards.

When the ball is projected downwards, the component of velocity in the positive-x direction will remain constant, whereas the velocity in the y direction will increase due to the gravitational pull. Therefore, the final velocity of the ball when it reaches the ground will be given by
$2as={{v}^{2}}-{{u}^{2}}$
$\Rightarrow {{v}^{2}}=2gs+{{u}^{2}}$
$\Rightarrow v=\sqrt{2gh+2gk}$
Where $h$ is the height of the building.
Now, the maximum distance that is travelled horizontally to reach Ram is
${{d}_{2}}=vt$
$\Rightarrow {{d}_{2}}=\left( \sqrt{2gh+2gk} \right)\cdot t$

PART 2: (projection from the ground to the top of the building)
Similarly, when the ball is projected in the upwards direction to reach Shyam who is at the top of the building, the component of velocity of the ball in the x direction is constant, whereas the final velocity of the ball in the y direction becomes.
$2as={{v}^{2}}-{{u}^{2}}$
$\Rightarrow {{v}^{2}}=2as+{{u}^{2}}$
$\Rightarrow v=\sqrt{-2gh+2gk}$
Here, the gravitational acceleration is taken negative as the ball is thrown upwards.
Now, the maximum distance from which Ram can throw the ball at Shyam becomes
${{d}_{1}}=vt $
$\Rightarrow {{d}_{1}}=\left( \sqrt{-2gh+2gk} \right)\cdot t$
Now, taking the ratio of both the equations obtained in both parts
$\dfrac{{{d}_{1}}}{{{d}_{2}}}=\left( \sqrt{\dfrac{2gk-2gh}{2gk+2gh}} \right)\cdot \dfrac{t}{t}$
$\therefore\dfrac{{{d}_{1}}}{{{d}_{2}}}=\sqrt{\dfrac{k-h}{k+h}}$

Hence, the correct answer is option B.

Note: The maximum distance travelled in the horizontal direction solely depends upon the magnitude of velocity in the y direction. Here we have to simply use the equation of motion instead of considering the formulas of projectile motion. Also here we have taken the displacement or the distance travelled by the ball as h which is approximation, as the height of both Shyam and Ram is not taken into consideration.