Question

Two persons are $a$ metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter person is.
(a) $\dfrac{a}{4}$
(b) $\dfrac{a}{\sqrt{2}}$
(c) $a\sqrt{2}$
(d) $\dfrac{a}{2\sqrt{2}}$

Answer 1

Hint: For solving this problem first we will draw the geometrical figure as per the given data. After that, we will use the basic formula of trigonometry $\tan \theta =\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)}$ and $\tan \left( \dfrac{\pi }{2}-\theta \right)=\cot \theta =\dfrac{1}{\tan \theta }$ . Then, we will solve correctly to get the height of the shorter person.

Complete step-by-step answer:
Given:
It is given that there are two persons $a$ metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary. And we have to find the height of the shorter person.
Now, first, we will draw a geometrical figure as per the given data. For more clarity look at the figure given below:

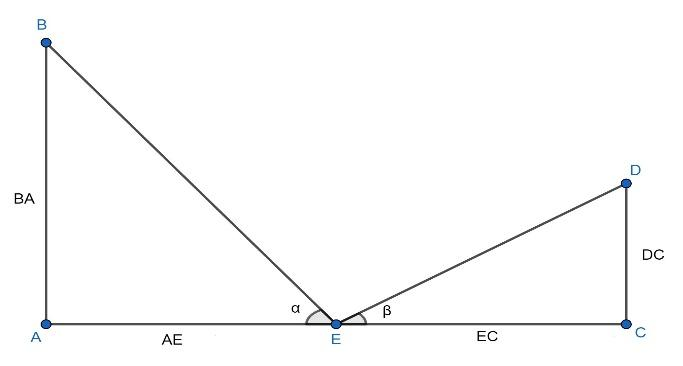
In the above figure BA represents the height of the taller person, DC represents the height of the shorter person and AC represents the distance between their feet so, $AC=a$ metres. And E is the midpoint of the AC so, $AE=EC=\dfrac{a}{2}$ metres. Moreover, $\alpha $ and $\beta $ are the angle of elevations of the topmost point of the taller and shorter person respectively and it is given that these angles are complementary so, the value of $\alpha +\beta =\dfrac{\pi }{2}$ .
Now, consider $\Delta ABE$ in which $\angle BAE={{90}^{0}}$ , AE is equal to the length of the base, BA is equal to the length of the perpendicular and $\angle BEA=\alpha $. Then,
$\begin{align}
  & \tan \left( \angle BEA \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\
 & \Rightarrow \tan \alpha =\dfrac{BA}{AE} \\
 & \Rightarrow \tan \alpha =\dfrac{2\left( BA \right)}{a}............................\left( 1 \right) \\
\end{align}$
Now, consider $\Delta CDE$ in which $\angle DCE={{90}^{0}}$ , EC is equal to the length of the base, DC is equal to the length of the perpendicular and $\angle DEC=\beta $. Then,

$\begin{align}
  & \tan \left( \angle DEC \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\
 & \Rightarrow \tan \beta =\dfrac{DC}{EC} \\
 & \Rightarrow \tan \beta =\dfrac{2\left( DC \right)}{a}............................\left( 2 \right) \\
\end{align}$
Now, as it is given that from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary. Then,
$\begin{align}
  & \alpha +\beta =\dfrac{\pi }{2} \\
 & \Rightarrow \alpha =\dfrac{\pi }{2}-\beta \\
 & \Rightarrow \tan \alpha =\tan \left( \dfrac{\pi }{2}-\beta \right) \\
 & \Rightarrow \tan \alpha =\cot \beta \\
 & \Rightarrow \tan \alpha =\dfrac{1}{\tan \beta } \\
 & \Rightarrow \tan \alpha \tan \beta =1 \\
\end{align}$
Now, substitute $\tan \alpha =\dfrac{2\left( BA \right)}{a}$ from equation (1) and $\tan \beta =\dfrac{2\left( DC \right)}{a}$ from equation (2) in the above equation. Then,
$\begin{align}
  & \tan \alpha \tan \beta =1 \\
 & \Rightarrow \dfrac{2\left( BA \right)}{a}\times \dfrac{2\left( DC \right)}{a}=1 \\
 & \Rightarrow \left( BA \right)\times \left( DC \right)=\dfrac{{{a}^{2}}}{4} \\
\end{align}$
Now, as BA represents the height of the taller person and DC represents the height of the shorter person. And it is given that the height of one is double that of the other so, we can substitute $BA=2\left( DC \right)$ in the above equation. Then,
$\begin{align}
  & \left( BA \right)\times \left( DC \right)=\dfrac{{{a}^{2}}}{4} \\
 & \Rightarrow 2{{\left( DC \right)}^{2}}=\dfrac{{{a}^{2}}}{4} \\
 & \Rightarrow {{\left( DC \right)}^{2}}=\dfrac{{{a}^{2}}}{8} \\
 & \Rightarrow DC=\dfrac{a}{2\sqrt{2}} \\
\end{align}$
Now, from the result, we conclude that the length of DC will be equal to $\dfrac{a}{2\sqrt{2}}$ metres.
Thus, the height of the shorter person will be $\dfrac{a}{2\sqrt{2}}$ metres.
Hence, (d) is the correct option.

Note: Here, the student should first try to understand what is asked in the problem. After that, we should try to draw the geometrical figure as per the given data. Moreover, we should apply the basic formula of trigonometry properly without any error and avoid calculation mistakes while solving to get the correct answer and then select the correct option.