Question

Two persons $A$ and $B$ start from the same location and walk around a square in opposite directions with constant speeds. The square has side $60m$. Speeds of $A$ and $B$ are $4m/s$ and $2m/s$ respectively. When will they meet for the first time?
A) 30 sec
B) 40 sec
C) 10 sec
D) 20 sec

Answer 1

Hint: To calculate the time taken, we have to consider the net sum of the distances travelled by both A and B. Then, we have to relate it to the perimeter of the square to obtain the time taken to cover the distance.

Complete step by step answer:
The rate of change of distance per unit time is called speed. However, the quantity speed is a scalar quantity. In order to consider the direction, we have to consider the quantity displacement instead of distance, which gives the relative change of the position of the object as opposed to the actual path taken for the change in the position of the object.
Here, we have another term called velocity which indicates the rate of displacement per unit time. The term velocity encompasses the direction of motion along with the magnitude of rate of motion.
Consider a square $\square abcd$ of side 60m as shown:

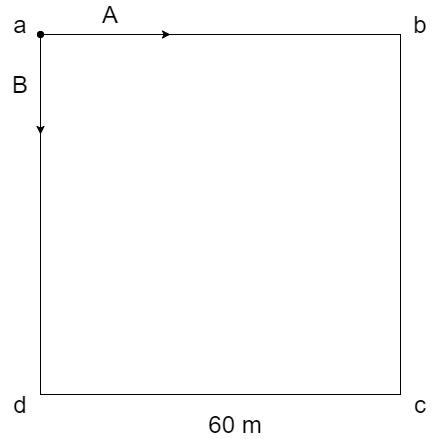
Two persons A and B start their journey at point $a$ and they move in opposite directions as indicated by arrows.
The point at which A and B meet is the point $c$.
When A and B travel to meet at this point $c$, each of them covers half of the perimeter of the square. Hence, the net distance covered by A and B is equal to the perimeter of the square.
Let time t be taken for A and B to meet since it is given that they meet at the same time.
Distance travelled by A is given by –
${d_A} = t{s_A}$
where ${s_A}$= speed of A, which is given as 4m/s.
Thus,
$\Rightarrow {d_A} = 4t$
Similarly, for B, we have –
$\Rightarrow {d_B} = 2t$
where the speed of B is given as 2m/s.
The total distance of A and B is equal to the perimeter of the square. Hence,
$\Rightarrow {d_A} + {d_B} = P$
Substituting,
$\Rightarrow 4t + 2t = 4 \times 60$
$ \Rightarrow 6t = 4 \times 60$
$ \Rightarrow t = 4 \times 10 = 40\sec $
Hence, A and B cross their path after 40 seconds from their start.

Hence, the correct option is Option B.

Note: In this problem, we have discussed the differences between the distance and displacement. To give you an example, in this problem, the distance travelled by A and B is equal to semi-perimeter or half-perimeter, which is equal to –
$2a = 2 \times 60 = 120m$
However, their displacement is equal to the diagonal of the square, which is equal to $a\sqrt 2 = 60\sqrt 2 = 84.85m$
Thus, we can clearly see the difference between the distance and displacement here.