
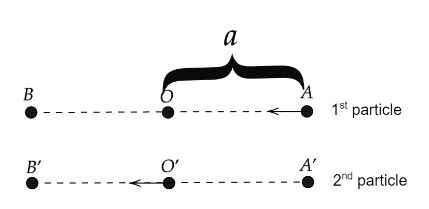
Two particles undergo SHM along parallel lines with the same time period (T) and equal amplitudes. At a particular instant, one particle is at its extreme position while the other is at its mean position. They move in the same direction. They will cross each other after a further time.

Answer
493.5k+ views
Hint: Two particles at different positions are in SHM, there must be some phase difference between them. So first we have to write the displacement equation for both the particles. Now at time zero we can find the phase difference between two positions. Now on equating the position we can find the time period after which they cross each other.
Complete step by step answer:
As per the problem we have two particles undergoing SHM along parallel lines with the same time period (T) and equal amplitudes. At a particular instant, one particle is at its extreme position while the other is at its mean position. They move in the same direction.We need to calculate the time period after which they will cross each other.
We know the equation of displacement,
1st particle at mean position hence we can write,
$y_1 = a\,\sin \omega t$
2nd particle at extreme position we can write,
$y_2 = a\,\sin \left( {\omega t + \phi } \right)$
Where, $a$ is the amplitude of the particle at SHM, $\omega $ is the angular frequency of the article and $\phi $ is the phase difference between two different positions.
To find the phase difference
Let $t = 0$ on both the position we will get,
$y_1 = a\,\sin \omega \left( 0 \right)$
$y_2 = a\,\sin \left( {\omega \left( 0 \right) + \phi } \right)$
$y_2 = a\,\sin \left( \phi \right)$
As the amplitude of two different position is a, we can now say that
$y_1 - y_2 = a$
Now on putting the value we will get,
$ - a\,\sin \left( \phi \right) = a$
Hence the phase difference $\phi = - \dfrac{\pi }{2}$.
Now on putting it in position 2 we will get,
$y_2 = a\,\sin \left( {\omega t - \dfrac{\pi }{2}} \right)$
We need to find the time period when two particles will cross each other.
To find this, the distance between two positions will be the same.
Hence,
$a\,\sin \omega t = a\,\sin \left( {\omega t - \dfrac{\pi }{2}} \right)$
We know that,
$\sin \left( {x - \dfrac{\pi }{2}} \right) = - \cos x$
Now we can write,
$a\,\sin \omega t = - a\,\cos \omega t$
Cancelling the common terms we will get,
$\sin \omega t = - \cos \omega t$
Rearranging and using trigonometric formula we will get,
$\tan \omega t = - 1$
$ \Rightarrow {\tan ^{ - 1}} - 1 = \omega t$
Now we know, ${\tan ^{ - 1}} - 1 = \dfrac{{3\pi }}{4}$
Hence,
$\omega t = \dfrac{{3\pi }}{4}$
We knew,
$\omega = \dfrac{{2\pi }}{T}$
Now putting the values we will get,
$\dfrac{{2\pi }}{T}t = \dfrac{{3\pi }}{4}$
Cancelling the common terms and rearranging we will get,
$\therefore t = \dfrac{{3T}}{8}$
Therefore, the two particles will cross each other after a further time of $\dfrac{{3T}}{8}$.
Note: We have taken the difference of two positions as ‘a’ because when a particle moves from one position to another then the particle has the same amplitude which is equal to a and hence there difference in distance is also a. SHM is a special type of period motion where the restoring force on the moving object is directly proportional to magnitude of displacement and acts towards object equilibrium position.
Complete step by step answer:
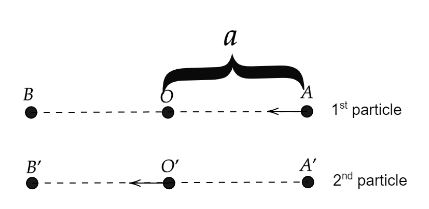
As per the problem we have two particles undergoing SHM along parallel lines with the same time period (T) and equal amplitudes. At a particular instant, one particle is at its extreme position while the other is at its mean position. They move in the same direction.We need to calculate the time period after which they will cross each other.

We know the equation of displacement,
1st particle at mean position hence we can write,
$y_1 = a\,\sin \omega t$
2nd particle at extreme position we can write,
$y_2 = a\,\sin \left( {\omega t + \phi } \right)$
Where, $a$ is the amplitude of the particle at SHM, $\omega $ is the angular frequency of the article and $\phi $ is the phase difference between two different positions.
To find the phase difference
Let $t = 0$ on both the position we will get,
$y_1 = a\,\sin \omega \left( 0 \right)$
$y_2 = a\,\sin \left( {\omega \left( 0 \right) + \phi } \right)$
$y_2 = a\,\sin \left( \phi \right)$
As the amplitude of two different position is a, we can now say that
$y_1 - y_2 = a$
Now on putting the value we will get,
$ - a\,\sin \left( \phi \right) = a$
Hence the phase difference $\phi = - \dfrac{\pi }{2}$.
Now on putting it in position 2 we will get,
$y_2 = a\,\sin \left( {\omega t - \dfrac{\pi }{2}} \right)$
We need to find the time period when two particles will cross each other.
To find this, the distance between two positions will be the same.
Hence,
$a\,\sin \omega t = a\,\sin \left( {\omega t - \dfrac{\pi }{2}} \right)$
We know that,
$\sin \left( {x - \dfrac{\pi }{2}} \right) = - \cos x$
Now we can write,
$a\,\sin \omega t = - a\,\cos \omega t$
Cancelling the common terms we will get,
$\sin \omega t = - \cos \omega t$
Rearranging and using trigonometric formula we will get,
$\tan \omega t = - 1$
$ \Rightarrow {\tan ^{ - 1}} - 1 = \omega t$
Now we know, ${\tan ^{ - 1}} - 1 = \dfrac{{3\pi }}{4}$
Hence,
$\omega t = \dfrac{{3\pi }}{4}$
We knew,
$\omega = \dfrac{{2\pi }}{T}$
Now putting the values we will get,
$\dfrac{{2\pi }}{T}t = \dfrac{{3\pi }}{4}$
Cancelling the common terms and rearranging we will get,
$\therefore t = \dfrac{{3T}}{8}$
Therefore, the two particles will cross each other after a further time of $\dfrac{{3T}}{8}$.
Note: We have taken the difference of two positions as ‘a’ because when a particle moves from one position to another then the particle has the same amplitude which is equal to a and hence there difference in distance is also a. SHM is a special type of period motion where the restoring force on the moving object is directly proportional to magnitude of displacement and acts towards object equilibrium position.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




