Question

Two particles of equal mass $m$ go around in a circle of radius $R$ under the action of their mutual gravitational attraction. The speed of each particle is $v$. Find the value of $v$.
A. $v=\dfrac{1}{2R}\sqrt{\left( \dfrac{1}{Gm} \right)}$
B. $v=\sqrt{\left( \dfrac{Gm}{2R} \right)}$
C. $v=\dfrac{1}{2}\sqrt{\left( \dfrac{Gm}{R} \right)}$
D. $v=\sqrt{\left( \dfrac{4Gm}{R} \right)}$

Answer 1

Hint: The gravitational attraction between the particles will contribute to the centrifugal force required for the circular motion. Find the gravitational force of attraction due to each other. Equate the value with the required centrifugal force to derive the expression of speed.

Formula Used:
Newton’s law of gravitation gives us the following equation,
$F=G\dfrac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}$,

Where,
$F$ is the gravitational force between the two particles,
$G$ is the universal gravitational constant
${{m}_{1}}$ is the mass of the first particle
${{m}_{2}}$is the mass of the second particle
$r$ is the distance between two particles.

The centrifugal force is given by,
$\dfrac{m{{v}^{2}}}{r}$
Where,
$m$ is the mass of the particle,
$v$ is the velocity of the particle,
$r$ is the radius of the circle.

Complete step by step answer:

Let’s understand the following figure first.

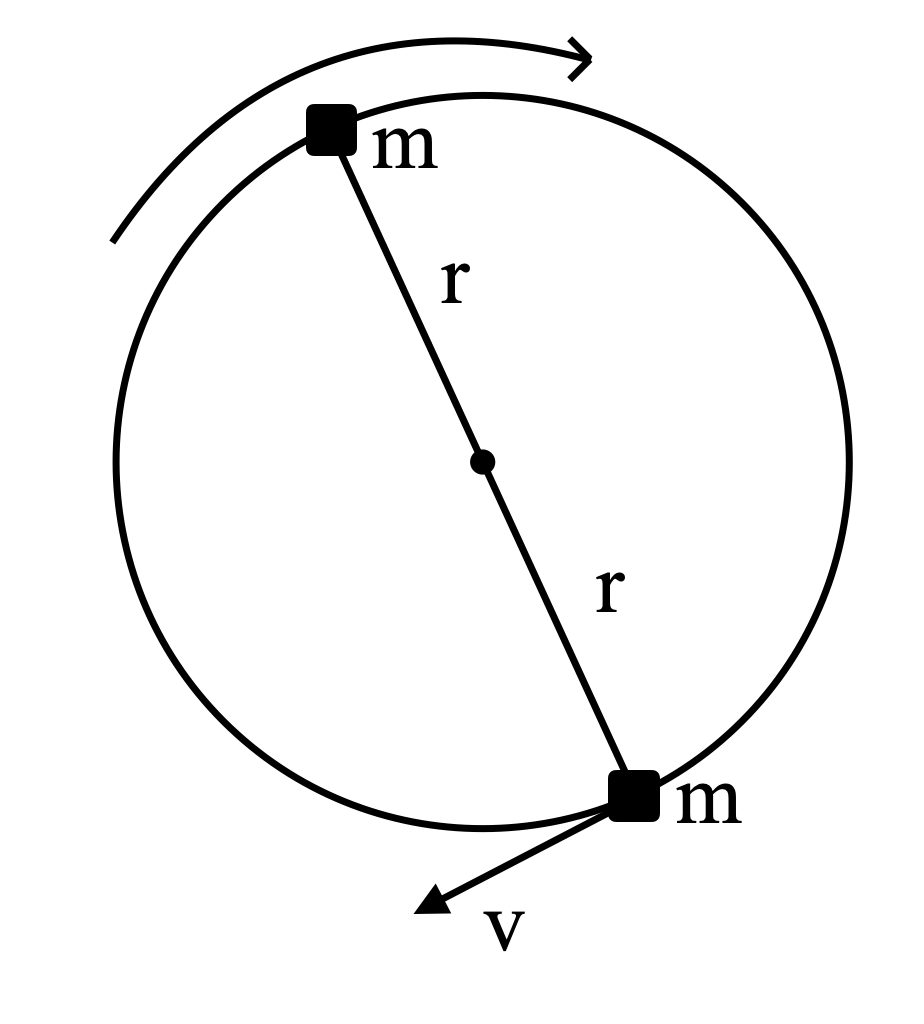
The two particles are moving in a circular motion in this way. As a result, the distance between the particles is,
$2r$
Hence the gravitational attraction between them is given by,
${{F}_{1}}=G\dfrac{m\times m}{{{(2R)}^{2}}}=\dfrac{G{{m}^{2}}}{4{{R}^{2}}}$


Now, let us consider the centrifugal force on the particle.

To continue the circular motion there must be a force which is equal to,
${{F}_{2}}=\dfrac{m{{v}^{2}}}{R}$

In this case, the gravitational force is contributing to the force.

We can consider a pseudo force working on the particle in the opposite direction, but it has the same magnitude.

Let’s look at the free-body diagram.

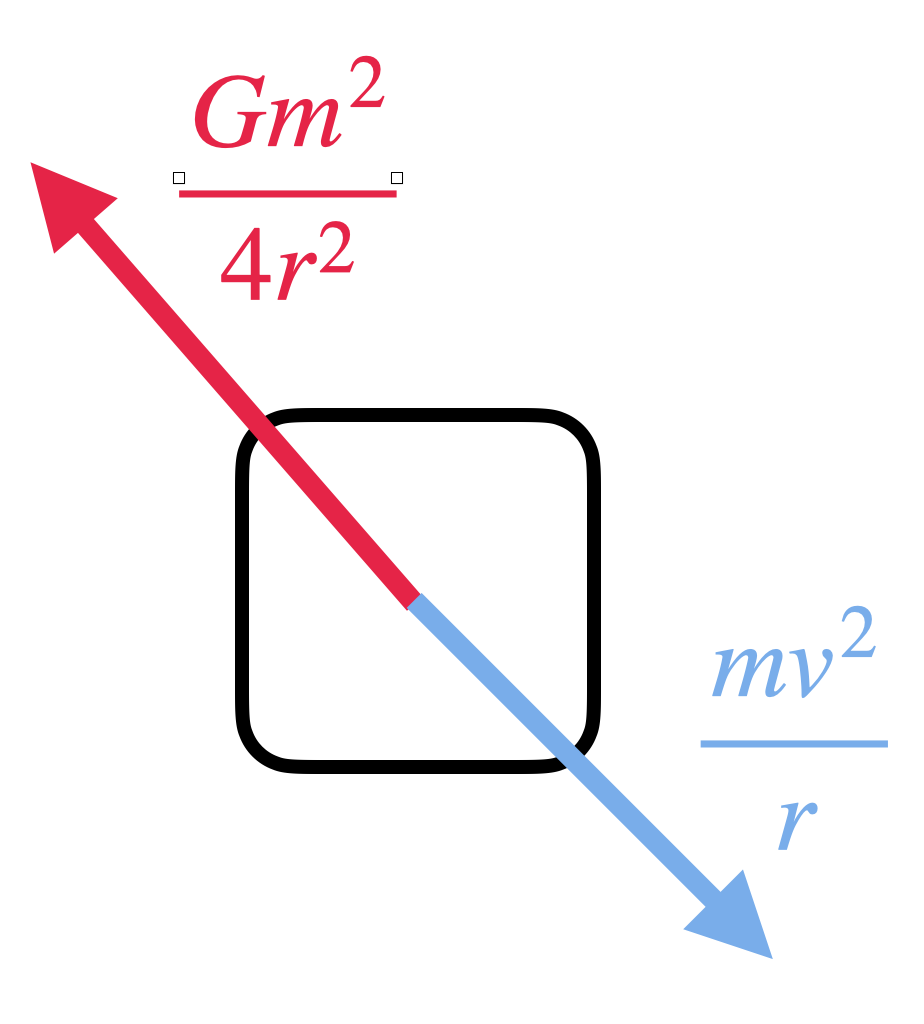
So, these two forces must be equal and opposite to maintain the circular motion of the particle.

Hence, we can write the equation,
${{F}_{1}}={{F}_{2}}$.
$\Rightarrow v=\dfrac{1}{2}\sqrt{\dfrac{Gm}{R}}$

$\Rightarrow {{v}^{2}}=\dfrac{Gm}{4R}$
$\Rightarrow v=\dfrac{1}{2}\sqrt{\dfrac{Gm}{R}}$
So, the correct option is (C).

Note: This problem was easy enough to complete without drawing the free body diagram (FBD). But it is a good practice to draw the FBD as we can incorporate all the forces in the same diagram.
If we don’t assume the effects of any other planets, the planetary motions are guided in a similar fashion. This problem is the basis of planetary motion.