Question

Two particles move at right angles to each other. Their de-Broglie wavelengths are ${{\lambda }_{1}}$ and ${{\lambda }_{2}}$ respectively. The particles are undergoing perfectly inelastic collisions. The de-Broglie wavelength $\lambda $, of the final particle, is found to be
$\begin{align}
  & A.\lambda =\dfrac{{{\lambda }_{1}}+{{\lambda }_{2}}}{2} \\
 & B.\dfrac{2}{\lambda }=\dfrac{1}{{{\lambda }_{1}}}+\dfrac{1}{{{\lambda }_{2}}} \\
 & C.\lambda =\sqrt{{{\lambda }_{1}}{{\lambda }_{2}}} \\
 & D.\dfrac{1}{{{\lambda }^{2}}}=\dfrac{1}{{{\lambda }_{1}}^{2}}+\dfrac{1}{{{\lambda }_{2}}^{2}} \\
\end{align}$

Answer 1

Hint: First of all find out the momentum of both the particles. Then apply the conservation of momentum in it. The total momentum we get will be a vector. The resultant of this should be found out. From there derive the expression needed. This all will help you in answering this question.

Complete step by step answer:
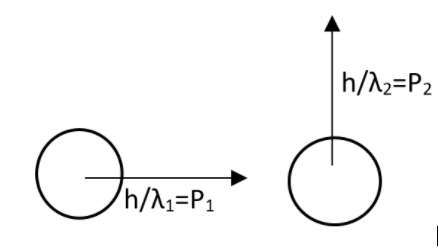
The momentum of the first particle is given as,
${{\vec{P}}_{1}}=\dfrac{h}{{{\lambda }_{1}}}\hat{i}$
Where $h$be the Planck’s constant.
The momentum of the second particle can be written as,
${{\vec{P}}_{2}}=\dfrac{h}{{{\lambda }_{2}}}\hat{j}$
Now we can apply the conservation of momentum in this system of particles. Therefore we can write that,
$\vec{P}={{\vec{P}}_{1}}+{{\vec{P}}_{2}}$
Substituting the values in it will give,
$\vec{P}=\dfrac{h}{{{\lambda }_{1}}}\hat{i}+\dfrac{h}{{{\lambda }_{2}}}\hat{j}$
Therefore the total momentum of the system of particles has been obtained. Now we have to find out the resultant of the momentum of the body. This can be written as,
$\left| {\vec{P}} \right|=\sqrt{{{\left( \dfrac{h}{{{\lambda }_{1}}} \right)}^{2}}+{{\left( \dfrac{h}{{{\lambda }_{2}}} \right)}^{2}}}$
The resultant momentum can be written as an equation given as,
$\vec{P}=\dfrac{h}{\lambda }$
Substituting this in the above mentioned equation will give,
\[\dfrac{h}{\lambda }=\sqrt{{{\left( \dfrac{h}{{{\lambda }_{1}}} \right)}^{2}}+{{\left( \dfrac{h}{{{\lambda }_{2}}} \right)}^{2}}}\]
All the common terms can be cancelled. Therefore we can write that,
\[\dfrac{1}{\lambda }=\sqrt{{{\left( \dfrac{1}{{{\lambda }_{1}}} \right)}^{2}}+{{\left( \dfrac{1}{{{\lambda }_{2}}} \right)}^{2}}}\]
The whole equation can be squared. Thus the equation will become,
\[\dfrac{1}{{{\lambda }^{2}}}=\dfrac{1}{{{\lambda }_{1}}^{2}}+\dfrac{1}{{{\lambda }_{2}}^{2}}\]
Therefore the answer has been calculated. It is given as option D.

Note:
According to the dual nature of a wave, the de Broglie wavelength is a wavelength associated with all the bodies in quantum mechanics which represents the probability density of detecting the particle at a specific point of the configuration space. The wavelength of a particle is found to be inversely proportional to the momentum of the particle.