Question

Two particles execute S.H.M along the same line at the same frequency. They move in opposite directions at the mean position. The phase difference will be:
A) $2\pi $
B) $\dfrac{{2\pi }}{3}$
C) $\pi $
D) $\dfrac{\pi }{2}$

Answer 1

Hint: S.H.M mentioned in the question means simple harmonic motion (a repetitive back and forth movement). The equations for displacement of both with some phase difference between them. When two particles are in opposite directions, the angle formed between them is $\pi $

Complete Step by step answer: The particles are executing Simple Harmonic Motion (S.H.M) along the same line with the same frequency. Their equations can be given as:
$
  x = {A_1}\sin \omega t \\
 \Rightarrow x = {A_2}\sin \left( {\omega t + \phi } \right) \\
 $
As their frequencies are the same, we can consider that they have the same displacement x. A denotes amplitude of respective particle and $\phi $ is the phase difference between these particles.
In SHM, they move from one extreme to another extreme position through the mean position. So, when they are at mean position there will be no displacement (x = 0).
For the first particle:
\[
  x = {A_1}\sin \omega t \\
  \Rightarrow 0 = {A_1}\sin \omega t \\
  \Rightarrow \sin \omega t = 0 \\
  \Rightarrow \omega t = {\sin ^{ - 1}}\left( 0 \right) \\
  \Rightarrow \omega t = 0\left( {\because \sin 0 = 0} \right)....(1) \\
 \]
For the second particle:
\[
  x = {A_2}\left( {\sin \omega t + \phi } \right) \\
 \Rightarrow 0 = {A_2}\left( {\sin \omega t + \phi } \right) \\
  \Rightarrow \omega t + \phi = 0 or \pi \\
 \]
As the particles are moving in the opposite directions, we can take their sum equal to $\pi $. Substituting value of $\omega t$ from (1), we get:
$
  0 + \phi = \pi \\
   \Rightarrow \phi = \pi \\
 $
Therefore, the phase difference between the two particles is $\pi $ and the correct option is C).

Note: The question can also be seen as:

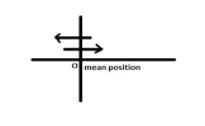
The motion of the particles at mean position is opposite in direction. In SHM, the particle makes angle $\pi $ from mean to extreme and back to mean position.
When the particle along positive direction of x – axis will be at the mean position (phase angle 0°) at that instant, the one along negative direction of x – axis would have gone to the extreme position and returned back to the mean position (phase 90° + 90° = 180° or $\pi $)
So the phase difference between the two particles become:
$\pi - 0 = \pi $