Question

Two particles are simultaneously projected in the horizontal direction from a point P at a certain height. The initial velocities of the particles are oppositely directed to each other and have magnitude v each. The separation between the particles at a time when their position vectors (drawn from the point P) are mutually perpendicular, is
A. $\dfrac{{{v^2}}}{{2g}}$
B. $\dfrac{{{v^2}}}{g}$
C. $\dfrac{{4{v^2}}}{g}$
D. $\dfrac{{2{v^2}}}{g}$

Answer 1

Hint: When two vectors are $\overrightarrow A $and $\overrightarrow B $are perpendicular to each other then, $\overrightarrow A \,.\,\overrightarrow B = 0$. The rate at which the two particles separate is known as velocity of separation.

Complete step by step solution:

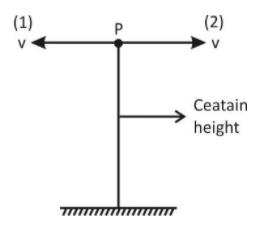
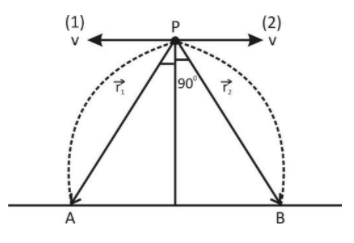
Let two particles named (1) and (2) respectively, are projected direction from point P with same velocity v but opposite in direction. Let after time `t’ the position vector of particle (1) and (2) are perpendicular with respect to point `P’ then the horizontal velocity tends to separate them and gravity moves in downward direction. So the position vector of particle (i) is given by,
$\overrightarrow {{r_1}} = {\overrightarrow r _{x1}} + {\overrightarrow r _{y1}}$
Where ${\overrightarrow r _{x1}}$ is displacement covered by particle $1$in horizontal/$x$ direction and ${\overrightarrow r _{y1}}$ is displacement covered by particle $1$ in vertical/$y$ direction.
$\overrightarrow {{r_1}} = vt\left( { - \widehat i} \right) + \left( {0 \times t + \dfrac{1}{2}g{t^2}} \right)\left( { - \widehat j} \right)$
$\overrightarrow {{r_1}} = - vt\widehat i - \dfrac{1}{2}g{t^2}\widehat j......\left( i \right)$
Now the position vector of second particle is given by,

$\overrightarrow {{r_2}} = {\overrightarrow r _{x2}} + {\overrightarrow r _{y2}}$
Where ${\overrightarrow r _{x2}} \to $displacement of particle $2$ in horizontal/$x$ direction and ${\overrightarrow r _{y2}} \to $ Displacement of particle $2$ in vertical/$y$ direction.
So, $\overrightarrow {{r_2}} = vt\left( { + \widehat i} \right) + \left( {0 + \dfrac{1}{2}g{t^2}} \right)\left( { - \widehat j} \right)$
$\overrightarrow {{r_2}} = vt\widehat i - \dfrac{1}{2}g{t^2}\widehat j$
If \[{\overrightarrow r _1} + {\overrightarrow r _2}\] after time ‘t’ then\[{\overrightarrow r _1} - {\overrightarrow r _2} = 0\]
$ \Rightarrow \left( { - vt\widehat i - \dfrac{1}{2}g{t^2}\widehat j} \right)\left( {vt\widehat i - \dfrac{1}{2}g{t^2}\widehat j} \right) = 0$
$ \Rightarrow {\left( {vt} \right)^2} + {\left( {\dfrac{1}{2}g{t^2}} \right)^2} = 0$
$ \Rightarrow {\left( {\dfrac{1}{2}g{t^2}} \right)^2} = {\left( {vt} \right)^2}$taking underfoot of both sides,
$ \Rightarrow \sqrt {{{\left( {\dfrac{1}{2}g{t^2}} \right)}^2}} = \sqrt {{{\left( {vt} \right)}^2}} $
$ \Rightarrow \dfrac{1}{2}g{t^2} = vt$
$ \Rightarrow \dfrac{{gt}}{2} = v \Rightarrow t = \dfrac{{2v}}{g}$
Now the velocity of separation of the particle (1) and (2)
$ = v + v = 2v$ so the separation between the particles at a time when their position vectors (drawn from the point P) are mutually perpendicular, is
AB $ = $Velocity of separation $ \times $time
AB \[ = \left( {2v} \right) \times t = 2v \times \dfrac{{2v}}{g}\]
AB $ = \dfrac{{4{v^2}}}{g}$

Hence, option (C) is correct.

Additional Information: The velocity of separation or approach is a component of relative velocity of one particle with respect to another.

Note: In this question the horizontal velocity makes effort to move the horizontal direction and that of gravity in downward direction so the displacement into particles is due to both.