Question

Two particles are in SHM in parallel straight lines close to each other. Amplitude A and time period T of both the particles are equal. At t=0, one particle is at displacement ${{x}_{1}}=+A$ and other at ${{x}_{2}}=-\dfrac{A}{2}$ and they are approaching towards each other, after what time they will cross each other?
A. $\dfrac{T}{3}$
B. $\dfrac{T}{4}$
C. $\dfrac{5T}{6}$
D. $\dfrac{T}{6}$

Answer 1

Hint: As a very first step, you will have to make a reference phase diagram for better understanding and also for an easier way to solve. There you will get the angular distance between the two particles. The midpoint of this distance will be the point at which they cross each other. You could find the time taken to reach that point accordingly.

Complete answer:
In the question, we have two particles that are moving in a straight line about an equilibrium position with same amplitude and time period. At time t=0 their displacements are given as, ${{y}_{1}}=+A$ and ${{y}_{2}}=-\dfrac{A}{2}$
So, let us make a reference phase diagram for the given two particles.

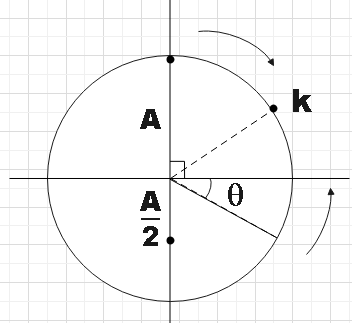
From the given reference phase diagram we see that,
$A\sin \theta =\dfrac{A}{2}$
$\Rightarrow \theta ={{\sin }^{-1}}\left( \dfrac{1}{2} \right)=30{}^\circ $ ………………………………………….. (1)
So the total angular distance between the two particles will be,
$\omega =90+30=120{}^\circ $
Since the time period is the same for both the given particles, the angular distance travelled by both of them to reach the point at which they cross each other will be the same. So, we need to find the midpoint between the initial positions of the two particles and that will be the point at which they cross each other,
$\omega '=60{}^\circ $
Let T be the time taken to travel$360{}^\circ $, so, the time taken to travel
$T\to 360{}^\circ $
$\Rightarrow 60{}^\circ \to \dfrac{T}{360}\times 60{}^\circ =\dfrac{T}{6}$
Therefore, we found that the given two particles cross each other at time $t=\dfrac{T}{6}s$ .

Note:
In case if you are wondering how the angular distance covered will be the same when the time period is same, recall the relation between $\omega $ and T given by,
$T=\dfrac{2\pi }{\omega }$
We have measured the angular distance from their respective initial positions as per the direction approach mentioned.