Question

Two opposite angles of a parallelogram are ${\left( {5x - 2} \right)^ \circ }$ and ${\left( {40 - x} \right)^ \circ }$ . Find the value of x.

Answer 1

Hint: We know that the opposite angles of a parallelogram are equal. So there are only 2 unique angles in a parallelogram. Here the two opposite angles, which are equal, are given and we have to solve for x and find the measure of these two opposite angles. Equate ${\left( {5x - 2} \right)^ \circ }$ and ${\left( {40 - x} \right)^ \circ }$to find the value of x.

Complete step-by-step answer:

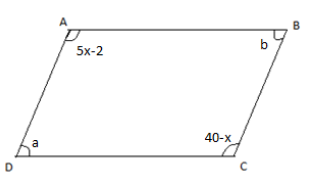
We are given that the two opposite angles of a parallelogram are ${\left( {5x - 2} \right)^ \circ }$ and ${\left( {40 - x} \right)^ \circ }$
We have to find the value of x.
As we can see in the diagram, in a parallelogram opposite angles are equal. Given angles are opposite so they are equal that is why we must equate one with another.
$5x - 2 = 40 - x$
Put all the x terms on the left hand side and all the constants on the right hand side.
$
  5x + x = 40 + 2 \\
  6x = 42 \\
 $
Divide 42 by 6 to get the value of x.
$
  x = \dfrac{{42}}{6} \\
  x = 7 \\
 $
Therefore, the value of x is 7.
Then the measure of the given angles will be 33 degrees.
$
  5x - 2 = 40 - x \\
  5\left( 7 \right) - 2 = 40 - 7 \\
  35 - 2 = 33 \\
  33 = 33 \\
 $
Sum of interior angles of a parallelogram is 360 degrees.
$
 33 + 33 + a + b = 360 \\
 a = b \\
 66 + 2a = 360 \\
 2a = 360 - 66 \\
 2a = 294 \\
 a = 147 \\
 a = b = 147 \\
 $
a=b because a and b are another set of opposite angles and are equal.
The measures of angles of parallelogram in degrees are 33, 147, 33 and 147.

Note: A parallelogram is a quadrilateral. The opposite sides of a parallelogram are parallel and equal and the opposite angles of a parallelogram are equal. The diagonals of a parallelogram bisect each other.