Question

Two non-mixing liquids of densities $\rho $ and $n\rho $ (n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL (p<1) in the denser liquid. The density d is equal to
\[\begin{array}{l}
A.\;\;\;\;\;\;\;\;\;\;\left\{ {1 + \left( {n - 1} \right)p} \right\}\;\rho \\
B.\;\;\;\;\;\;\;\;\;\;\left\{ {1 + \left( {n + 1} \right)p} \right\}\;\rho \\
C.\;\;\;\;\;\;\;\;\;\;\left\{ {2 + \left( {n + 1} \right)p} \right\}\;\rho \\
D.\;\;\;\;\;\;\;\;\;\;\left\{ {2 + \left( {n - 1} \right)p} \right\}\;\rho
\end{array}\]

Answer 1

Hint: As we go deeper in any liquid, the pressure increases, this increased pressure applies an upward force which balances the weight of liquid. If an object is floating in it, this extra force will balance the weight of this object. We can make use of this relation to find the density of the object immersed in liquid.

Complete step-by-step answer:
The liquid with greater density will be at the bottom and the cylinder will be suspended between the two liquids with some length in both of them.

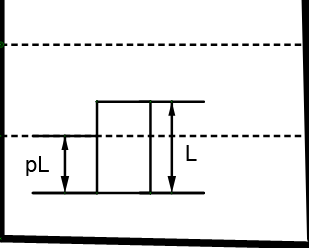
The weight of this cylinder will be balanced by the increased pressure at its bottom if we draw its free body diagram, we will have

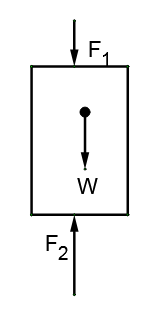
where ${F_1}$ is the force on its top surface due to liquid, ${F_2}$ is the force on its top surface due to liquid & W is the weight of the cylinder
If we consider pressure at the top surface of cylinder P and area of cylinder A, we can write
${F_1} = PA$
We know that if we go h height lower in the liquid of density$\rho $, its pressure increases by $\rho gh$
So, the pressure at the bottom of the first liquid will be
$P + \rho g\left( {L - pL} \right)$
So, the pressure at the bottom of the second liquid will be
$P + \rho g\left( {L - pL} \right) + n\rho g \times pL$
So ${F_2}$can be written as
${F_2} = \left( {P + \rho g\left( {L - pL} \right) + n\rho g \times pL} \right) \times A$
Also weight of the cylinder is
$W = d \times A \times L \times g$
Now, since the cylinder is in equilibrium, the net force on it must be zero
$\begin{array}{l}
{F_2} - {F_1} = W\\
\left( {P + \rho g\left( {L - pL} \right) + n\rho g \times pL} \right)A - PA = d \times A \times L \times g\\
 \Rightarrow PA + A\rho g\left( {L - pL} \right) + n\rho g \times pLA - PA = dALg\\
 \Rightarrow A\rho gL - A\rho gpL + n\rho gpLA = dALg\\
 \Rightarrow \rho - \rho p + n\rho p = d\\
 \Rightarrow d = \rho \left( {1 - p + np} \right)\\
 \Rightarrow d = \rho \left[ {1 + \left( {n - 1} \right)p} \right]
\end{array}$
So the correct option is A.

Note: The question can also be done by equating the weight of the cylinder with buoyant force due to two liquids. This approach will land us to the same equation as we got through this method (equation 1). In the second method, one must remember to add buoyant force due to the upper liquid too.