
Two moles of Helium gas are to be taken over the cycle \[{\text{ABCDA}}\]as shown (below) in the \[{\text{P - T}}\]diagram. (Assume the gas to be ideal and R is a gas constant.).
Now, match list I with list II and select the option given below:
List-1 List-2 \[{\text{(P)}}\] Magnitude of the work done by the gas is taking from \[{\text{A to B}}\] \[(1)\] \[{\text{693 R}}\] \[{\text{(Q)}}\] Magnitude of the work done by the gas is taking from \[{\text{B to C}}\] \[(2)\] \[{\text{277 R}}\] \[{\text{(R)}}\] Magnitude of the work done by the gas is taking from \[{\text{D to A}}\] \[(3)\] \[{\text{400 R}}\] \[{\text{(S)}}\] Magnitude of the net heat absorbed/evolved in the cycle \[{\text{ABCDA}}\] \[(4)\] \[{\text{416 R}}\]
A.\[{\text{P - 1, Q - 2, R - 3, S - 4}}\]
B.\[{\text{P - 3, Q - 2, R - 4, S - 3}}\]
C.\[{\text{P - 3, Q - 1, R - 4, S - 2}}\]
D.\[{\text{P - 4, Q - 3, R - 1, S - 2}}\]
| List-1 | List-2 | ||
| \[{\text{(P)}}\] | Magnitude of the work done by the gas is taking from \[{\text{A to B}}\] | \[(1)\] | \[{\text{693 R}}\] |
| \[{\text{(Q)}}\] | Magnitude of the work done by the gas is taking from \[{\text{B to C}}\] | \[(2)\] | \[{\text{277 R}}\] |
| \[{\text{(R)}}\] | Magnitude of the work done by the gas is taking from \[{\text{D to A}}\] | \[(3)\] | \[{\text{400 R}}\] |
| \[{\text{(S)}}\] | Magnitude of the net heat absorbed/evolved in the cycle \[{\text{ABCDA}}\] | \[(4)\] | \[{\text{416 R}}\] |

Answer
576k+ views
Hint:Hint: This question is based on the thermodynamic process. The process \[{\text{A to B}}\] and \[{\text{C to D}}\] is an isobaric process. The process \[{\text{B to C}}\] and \[{\text{D to A}}\] are isothermal processes. We need to use the required formula of work in each of the cases and we will get work done for each process.
Formula used:
For isobaric process \[{\text{W = - nR(}}{{\text{T}}_2} - {{\text{T}}_{\text{1}}}{\text{)}}\]
Where, \[{\text{W}}\] is work done, \[{\text{n}}\] is number of moles, \[{\text{R}}\] is universal gas constant and \[{{\text{T}}_2}{\text{ and }}{{\text{T}}_{\text{1}}}\] are final and initial temperature respectively.
For isothermal process \[{\text{W = - 2}}{\text{.303nRT log}}\dfrac{{{{\text{P}}_{\text{1}}}}}{{{{\text{P}}_{\text{2}}}}}\]
Where, \[{\text{W}}\] is work done, \[{\text{n}}\] is number of moles, \[{\text{R}}\] is universal gas constant and \[{{\text{P}}_{\text{2}}}{\text{ and }}{{\text{P}}_{\text{1}}}\] are final and initial pressure respectively.
Complete step by step answer:
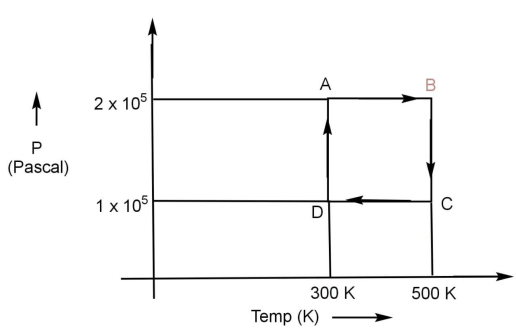
Let us understand the diagram first:
On the \[x\] axis of the graph temperature in \[{\text{K}}\] has been plotted and on \[y\] axis pressure in \[{\text{Pa}}\]has been plotted. So this is a \[{\text{P - T}}\] curve. The coordinates of points will give us the value of volume and pressure. If we look at the diagram point A cuts \[x\] axis at point 300 that means the temperature of gas at point A will be \[{{\text{T}}_{\text{A}}}{\text{ = 300 K}}\] and it cut \[y\] axis at point \[{{ 2 \times 1}}{{\text{0}}^5}\], so the pressure at point A will be \[{{\text{P}}_{\text{A}}}{{ = 2 \times 1}}{{\text{0}}^5}{\text{ Pa}}\]. Similarly we can do this for other, let us write down the value of temperature and pressure at every stage:
\[{{\text{T}}_{\text{A}}}{\text{ = 300 K and }}{{\text{P}}_{\text{A}}}{{ = 2 \times 1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\]
\[{{\text{T}}_{\text{B}}}{\text{ = 500 K and }}{{\text{P}}_{\text{B}}}{{ = 2 \times 1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\]
\[{{\text{T}}_{\text{C}}}{\text{ = 500 K and }}{{\text{P}}_{\text{C}}}{{ = 1 \times 1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\]
\[{{\text{T}}_{\text{D}}}{\text{ = 300 K and }}{{\text{P}}_{\text{D}}}{{ = 1 \times 1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\]
Using the respective equations for the process happening we will calculate the work done as follow:
The process \[A \to B\] is isobaric:
\[{{\text{W}}_{{\text{A}} \to {\text{B}}}} = {\text{nR}}({{\text{T}}_2} - {{\text{T}}_{\text{1}}})\]
\[ \Rightarrow {{\text{W}}_{{\text{A}} \to {\text{B}}}} = 2{\text{R}}(500 - 300) = 400{\text{R}}\]
The process \[B \to C\] is isothermal process:
\[{{\text{W}}_{{\text{B}} \to {\text{C}}}} = - {\text{2}}{\text{.303nRT log}}\dfrac{{{{\text{P}}_{\text{1}}}}}{{{{\text{P}}_2}}}\]
\[ \Rightarrow {{\text{W}}_{{\text{B}} \to {\text{C}}}} = - {\text{2}}{\text{.303}} \times {\text{2}} \times {\text{R}} \times {\text{500 log}}\dfrac{{2 \times {{10}^5}}}{{1 \times {{10}^5}}} = - 693{\text{R}}\]
The process \[C \to D\] is isobaric:
\[{{\text{W}}_{{\text{C}} \to {\text{D}}}} = {\text{nR(}}{{\text{T}}_2} - {{\text{T}}_1})\]
\[ \Rightarrow {{\text{W}}_{{\text{C}} \to {\text{D}}}} = 2{\text{R}}(300 - 500) = - 400{\text{R}}\]
The process \[D \to A\] is isothermal process:
\[{{\text{W}}_{{\text{D}} \to {\text{A}}}} = - {\text{2}}{\text{.303nRT log}}\dfrac{{{{\text{P}}_{\text{1}}}}}{{{{\text{P}}_2}}}\]
\[ \Rightarrow {{\text{W}}_{{\text{D}} \to {\text{A}}}} = - {\text{2}}{\text{.303}} \times {\text{2}} \times {\text{R}} \times 3{\text{00 log}}\dfrac{{1 \times {{10}^5}}}{{2 \times {{10}^5}}} = 416{\text{R}}\]
Total work done can be calculated by adding all the four work which will come out to be
\[{\text{W}} = 400{\text{R}} - 693{\text{R}} - 400{\text{R}} + 416{\text{R}} = - 277{\text{R}}\]
All the above data matches well with option C.
Note:
Isobaric process is the process in which the pressure remains constant; since bar is a unit of pressure we can easily remember that in isobaric process pressure remains constant. Isothermal process is the process in which temperature remains constant. We will ignore the negative sign here because this indicates the direction of reaction and heat changes.
Formula used:
For isobaric process \[{\text{W = - nR(}}{{\text{T}}_2} - {{\text{T}}_{\text{1}}}{\text{)}}\]
Where, \[{\text{W}}\] is work done, \[{\text{n}}\] is number of moles, \[{\text{R}}\] is universal gas constant and \[{{\text{T}}_2}{\text{ and }}{{\text{T}}_{\text{1}}}\] are final and initial temperature respectively.
For isothermal process \[{\text{W = - 2}}{\text{.303nRT log}}\dfrac{{{{\text{P}}_{\text{1}}}}}{{{{\text{P}}_{\text{2}}}}}\]
Where, \[{\text{W}}\] is work done, \[{\text{n}}\] is number of moles, \[{\text{R}}\] is universal gas constant and \[{{\text{P}}_{\text{2}}}{\text{ and }}{{\text{P}}_{\text{1}}}\] are final and initial pressure respectively.
Complete step by step answer:
Let us understand the diagram first:
On the \[x\] axis of the graph temperature in \[{\text{K}}\] has been plotted and on \[y\] axis pressure in \[{\text{Pa}}\]has been plotted. So this is a \[{\text{P - T}}\] curve. The coordinates of points will give us the value of volume and pressure. If we look at the diagram point A cuts \[x\] axis at point 300 that means the temperature of gas at point A will be \[{{\text{T}}_{\text{A}}}{\text{ = 300 K}}\] and it cut \[y\] axis at point \[{{ 2 \times 1}}{{\text{0}}^5}\], so the pressure at point A will be \[{{\text{P}}_{\text{A}}}{{ = 2 \times 1}}{{\text{0}}^5}{\text{ Pa}}\]. Similarly we can do this for other, let us write down the value of temperature and pressure at every stage:
\[{{\text{T}}_{\text{A}}}{\text{ = 300 K and }}{{\text{P}}_{\text{A}}}{{ = 2 \times 1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\]
\[{{\text{T}}_{\text{B}}}{\text{ = 500 K and }}{{\text{P}}_{\text{B}}}{{ = 2 \times 1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\]
\[{{\text{T}}_{\text{C}}}{\text{ = 500 K and }}{{\text{P}}_{\text{C}}}{{ = 1 \times 1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\]
\[{{\text{T}}_{\text{D}}}{\text{ = 300 K and }}{{\text{P}}_{\text{D}}}{{ = 1 \times 1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\]
Using the respective equations for the process happening we will calculate the work done as follow:
The process \[A \to B\] is isobaric:
\[{{\text{W}}_{{\text{A}} \to {\text{B}}}} = {\text{nR}}({{\text{T}}_2} - {{\text{T}}_{\text{1}}})\]
\[ \Rightarrow {{\text{W}}_{{\text{A}} \to {\text{B}}}} = 2{\text{R}}(500 - 300) = 400{\text{R}}\]
The process \[B \to C\] is isothermal process:
\[{{\text{W}}_{{\text{B}} \to {\text{C}}}} = - {\text{2}}{\text{.303nRT log}}\dfrac{{{{\text{P}}_{\text{1}}}}}{{{{\text{P}}_2}}}\]
\[ \Rightarrow {{\text{W}}_{{\text{B}} \to {\text{C}}}} = - {\text{2}}{\text{.303}} \times {\text{2}} \times {\text{R}} \times {\text{500 log}}\dfrac{{2 \times {{10}^5}}}{{1 \times {{10}^5}}} = - 693{\text{R}}\]
The process \[C \to D\] is isobaric:
\[{{\text{W}}_{{\text{C}} \to {\text{D}}}} = {\text{nR(}}{{\text{T}}_2} - {{\text{T}}_1})\]
\[ \Rightarrow {{\text{W}}_{{\text{C}} \to {\text{D}}}} = 2{\text{R}}(300 - 500) = - 400{\text{R}}\]
The process \[D \to A\] is isothermal process:
\[{{\text{W}}_{{\text{D}} \to {\text{A}}}} = - {\text{2}}{\text{.303nRT log}}\dfrac{{{{\text{P}}_{\text{1}}}}}{{{{\text{P}}_2}}}\]
\[ \Rightarrow {{\text{W}}_{{\text{D}} \to {\text{A}}}} = - {\text{2}}{\text{.303}} \times {\text{2}} \times {\text{R}} \times 3{\text{00 log}}\dfrac{{1 \times {{10}^5}}}{{2 \times {{10}^5}}} = 416{\text{R}}\]
Total work done can be calculated by adding all the four work which will come out to be
\[{\text{W}} = 400{\text{R}} - 693{\text{R}} - 400{\text{R}} + 416{\text{R}} = - 277{\text{R}}\]
All the above data matches well with option C.
Note:
Isobaric process is the process in which the pressure remains constant; since bar is a unit of pressure we can easily remember that in isobaric process pressure remains constant. Isothermal process is the process in which temperature remains constant. We will ignore the negative sign here because this indicates the direction of reaction and heat changes.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




