Question

Two men support a uniform horizontal rod at its two ends. If one of them suddenly lets go, the force exerted by the rod on the other man will
A. remain unaffected
B. Increase
C. Decrease
D. Become unequal to the force exerted by him on the beam.

Answer 1

Hint: Initially, reaction forces applied by both of the men were equal and the system was in complete rotational and translational equilibrium. Later, it will suffer a rotation as one of the men left.
Formula used:
Torque acting on a body, about an axis is:
$\tau = I \alpha$
and also as,
$\tau = rF$
where F is the force acting at a distance r (perpendicular) from the axis.
The moment of inertia of a rod about its end point is:
$I = \dfrac{ML^2}{3}$.

Complete answer:
Assume the mass of the rod as M and the length of the rod as L. The weight of the rod is W = Mg.

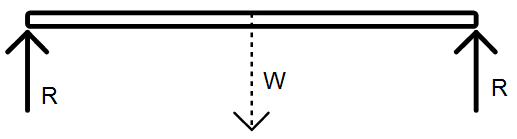
Initially, translational equilibrium gives us following expression:
$R + R - W = 0 $
where reaction force upwards is taken positive and weight downwards is taken negative.
We may write:
$R = \dfrac{W}{2}$.
Now, one of the ends has no reaction force upwards so for another man, who is still holding, the reaction force is R'.

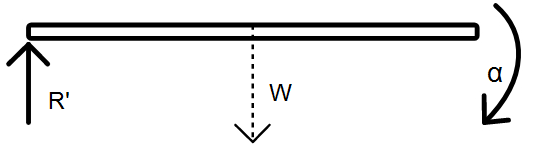
A torque will act due to the weight of the rod downwards. The angular acceleration of the rod can be found by equating two expressions for torque:
$Mg \times \dfrac{L}{2} = \dfrac{ML^2}{3} \times \alpha$.
Therefore,
$\alpha = \dfrac{3g}{2L} $.
Now, angular acceleration is related to linear acceleration as:
$ a = r \alpha $.
So, we may write
$a = \dfrac{\alpha L}{2}$.
By, the free body diagram of the rod, we may write:
$Mg - R' = Ma$
where Ma is the resultant force of the rod downwards.
Therefore, after substituting appropriate values, we may write:
$ R' = Mg - \dfrac{ 3 Mg}{4} = \dfrac{ Mg}{4} $.
We can see that we started with the R = W/2 reaction and we ended up with R' = W/4.

So, the correct answer is “Option C”.

Note:
The linear acceleration of the rod is dependent on the distance of the concerned point from the axis. We considered the axis to be another end point of the rod and the distance of the center of the rod from it were taken to be L/2.