Question

Two massless and friction pulleys A and B are connected as shown in the figure and the weight of $200 $ Kg is suspended from the third pulley system is in equilibrium by applying force F. The tension at point X of the string is

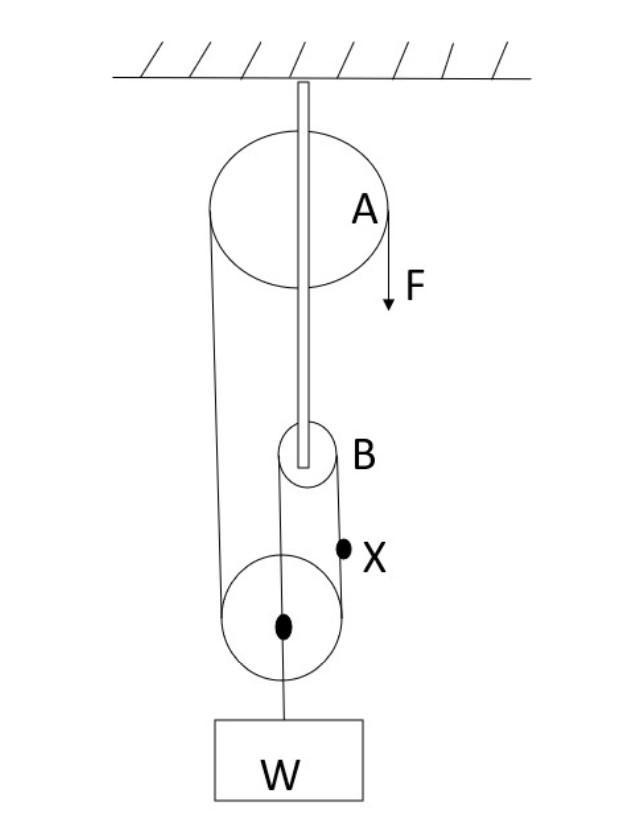
Answer 1

Hint: Pulleys are frictionless and massless, so we neglect friction forces and the mass of the pulley. Our first work is to find the direction of tension Keep in mind that tension is in the direction of the rope. After drawing the direction of tension, balance all the forces.

Complete answer:
Given that mass suspended from the third pulley system is $200$ Kg and is in equilibrium by applying force F. Make tension in the direction of rope as shown in the figure below. Now balance all the forces.

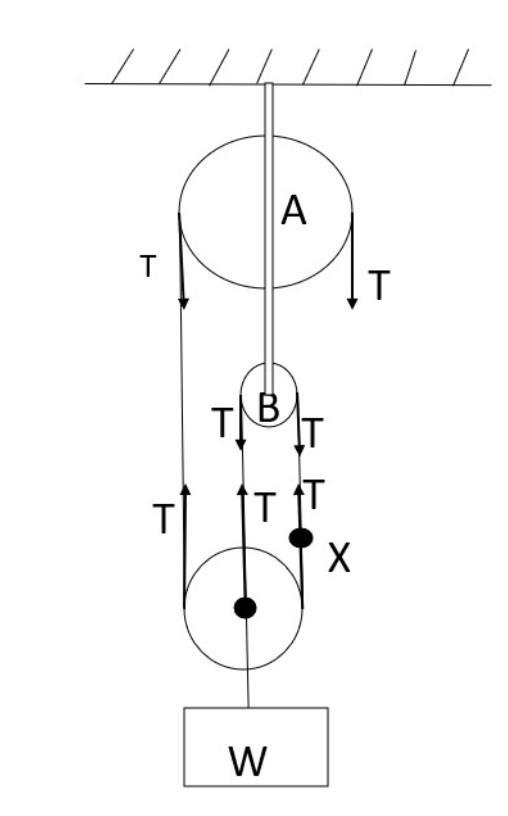
Tension along the same pulley will remain the same (constant). So, Tension along pulley A will cancel each other and similarly, Tension along pulley B will cancel each other.
Now, we are balancing the forces for obtaining equilibrium condition—
W is the weight and it is equal to the W =mass $\times $ gravity.
$ W = 200× 9.8 = 1960 N$
 $3 T = W
 T =\dfrac {W}{3}
 So, T =\dfrac {1960}{3} = 653.33 N$
Additional Information: - We assume the string to be ideal so that the force along the whole string is the same. Tension is along the rope and If the string is supposed to be massless and frictionless, then the pulling force at both ends of the string needs to be the same in magnitude

Note:
In this ques mass is given but during balancing the force weight will be taken because units of force and weight are the same. So, we need to get the weight by multiplying gravity with the mass. At equilibrium, an upward force is equal to the downward force to make the body stable.