Question

Two masses ${M_1} = 5kg$ and ${M_2} = 10kg$ are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When the masses are released, then the acceleration of the masses will be:

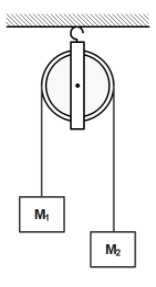
A. $g$
B. $\dfrac{g}{2}$
C. $\dfrac{g}{3}$
D. $\dfrac{g}{4}$

Answer 1

Hint: In the question, they’ve given a mass-pulley system, with masses, ${M_1}$ = 5kg and ${M_2}$ = 10kg. As ${M_2}$ > ${M_1}$ the acceleration of the second mass, ${M_2}$ will be downward while the acceleration of the ${M_1}$ will be upward. One can write the acceleration of the masses, with the help of Newton’s 2nd law. Solving these equations, we can find the acceleration of the masses.

Formula used:
$a = g\dfrac{{\left( {{M_2} - {M_1}} \right)}}{{{M_1} + {M_2}}}$

Complete answer:
The forces acting on the masses are the tension of the string and the weight of the blocks in a downward direction. The free-body diagrams of each of the blocks will be

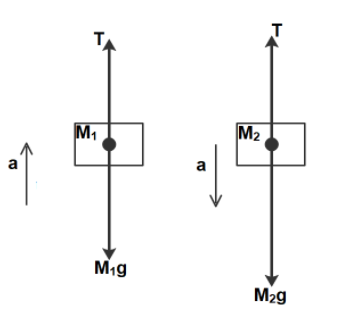
For the block of mass ${M_1}$, the forces acting are weight ${M_1}$g in the downward direction and the tension T in the upward direction. One can see that, ${M_1}$ < ${M_2}$ from the data given in the question. Let us say that ‘$a$’ is the acceleration of the block in an upward direction. According to Newton’s 2nd law, it will be given by
${M_1}a = T - {M_1}g - - > eq.1$
Similarly, for the second mass ‘$a$’ will be the acceleration in the downward direction. Applying the newton’s second law, we’ll have
${M_2}a = {M_2}g - T - - > eq.2$
Adding equation 1 and 2, we get
$\eqalign{
  & {M_1}a + {M_2}a = {M_2}g - {M_1}g \cr
  & \Rightarrow a = g\dfrac{{\left( {{M_2} - {M_1}} \right)}}{{{M_1} + {M_2}}} \cr} $
Substituting the values of ${M_1}$ = 5kg and ${M_2}$ = 10kg,
$\eqalign{
  & a = g\dfrac{{\left( {{M_2} - {M_1}} \right)}}{{{M_1} + {M_2}}} \cr
  & \Rightarrow a = g \times \dfrac{{\left( {10 - 5} \right)}}{{10 + 5}} \cr
  & \Rightarrow a = g \times \dfrac{5}{{15}} \cr
  & \Rightarrow a = \dfrac{g}{3} \cr} $

Therefore, the correct option is C.

Note:
Please note that a single string will only have the same tension all over the string. That is, it will be constant across the string, on either side. The acceleration of the system will be the same for both the masses, as we’re assuming the string to be rigid. Always try to incorporate a free body diagram into problems involving mechanics, as it helps you in understanding the direction of net force and the direction of acceleration.