Question

Two masses M and m are connected at two ends of an inextensible string. The string passes over a smooth frictionless pulley. Obtain the expression for acceleration of the masses and the tension in the string. Given M>m.

Answer 1

Hint: We can solve the given question with the help of a free body diagram. Here, we can find the forces acting on each of the bodies and in the entire system. We can derive equations of equivalent forces from the tension and the gravitational force that acts on the system.

Step by step answer:
The basic formula of force is used throughout this question that is:
\[force=mass\times acceleration\]
The other formulas are deduced from the equivalent forces acting on a body.
We are given two masses m and M where the mass of M is greater than that of m. It is connected to a string that passes through a smooth pulley. Hence, frictional force is absent. The gravitational force and the uniformly distributed tension on the string is present in the system and it is represented in the diagram.

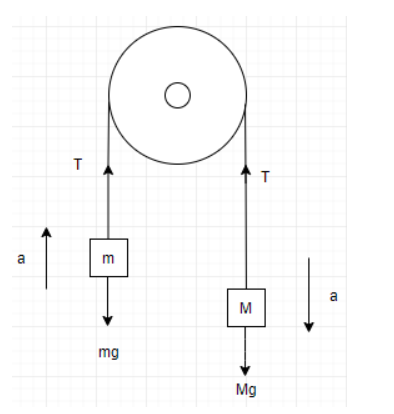
For mass m, the forces are given as
$\
   T-mg=ma \\
   \\
$
$\Rightarrow T=mg+ma=m(g+a)$ ………….(1)

For mass M, the forces are given as
$Mg-T=Ma$ …… (2)
Substituting (1) in (2), we get
$
   Mg-m(g+a)=Ma \\
  \Rightarrow Mg-mg-ma=Ma \\
  \Rightarrow (M-m)g=(M+m)a \\
  \therefore a=\dfrac{(M-m)g}{(M+m)} \\
$
Substituting the value of a to the previous equation,
$
   T=m(\dfrac{M-m}{M+m})g+mg $
$ \therefore T=\dfrac{Mm-{{m}^{2}}}{M+m}g+mg $
  $\therefore T=g(\dfrac{Mm-{{m}^{2}}}{M+m}+m)=g(\dfrac{Mm-{{m}^{2}}+{{m}^{2}}+Mm}{M+m})=g(\dfrac{2Mm}{M+m}) \\
$
Hence, we have obtained the values of both the tension in the string as well as the acceleration of the masses.

Note: The most important thing while solving such questions is the free body diagram.Free body diagram is defined as a graphical illustration or the representation of the forces that are applied, moments and the resultants. It is helpful to solve both simple and complex problems in mechanics.