Question

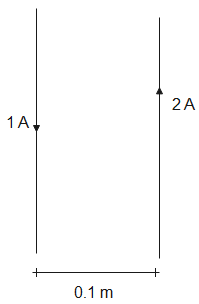
Two long parallel wires separated by $0.1m$ carry currents of $1A$ and $2A$ respectively in opposite directions. A third current carrying wire parallel to both of them is placed in the same plane such that it feels no net magnetic force. It is kept at a distance of-
(A). $0.5m$ from the ${{1}^{st}}$ towards the${{2}^{nd}}$ wire
(B). $0.2m$ from the ${{1}^{st}}$ towards the ${{2}^{nd}}$ wire
(C). $0.1m$ from the ${{1}^{st}}$, away from the ${{2}^{nd}}$ wire
(D).$0.2m$ from the ${{1}^{st}}$, away from the ${{2}^{nd}}$ wire

Answer 1

Hint: Since the current is flowing in opposite directions, the force acting due to each is in the opposite direction when the third wire is kept near one of the wires but the force acting on it is in the same direction when it is kept between them. The force due to the magnetic field of a current carrying wire depends on the surrounding medium, current flowing through it and the current of wire on which it acts and the distance between them.
Formulas used:
$B=\dfrac{{{\mu }_{0}}I}{2\pi r}$
$F=\dfrac{{{\mu }_{0}}{{I}_{1}}{{I}_{2}}}{2\pi r}$

Complete answer:
A magnetic field develops around a current carrying wire. The magnetic force due to a wire carrying current is given by-
$B=\dfrac{{{\mu }_{0}}I}{2\pi r}$
Here, $B$ is the magnetic field due to wire
${{\mu }_{0}}$ is the permittivity of free space
 $I$ is the current flowing through the wire
$r$ is distance from the wire
The force exerted due to a current carrying wire is-
$F=\dfrac{{{\mu }_{0}}{{I}_{1}}{{I}_{2}}}{2\pi r}$
Here, ${{I}_{1}}$ is the current flowing through one wire
${{I}_{2}}$ is current flowing through the other wire
$r$ is the distance between the two wires

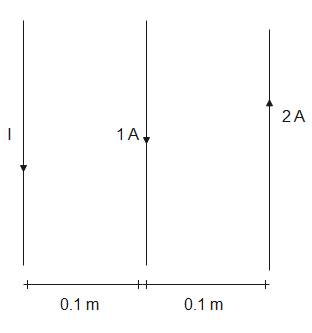
Given, a current carrying wire is kept some distance from two other current carrying wires such that no net force acts on it. Let it be at $x\,m$ from the wire carrying current $1A$, then its distance from the other wire will be $0.1+x$
Force due to wire carrying $1A$ current, ${{F}_{1}}$ will be-
${{F}_{1}}=\dfrac{{{\mu }_{0}}\times 1\times I}{2\pi x}$ - (1)
Force due to wire carrying $2A$ current, ${{F}_{2}}$ will be-
${{F}_{2}}=\dfrac{{{\mu }_{0}}\times 2\times I}{2\pi (0.1+x)}$ - (2)
By right hand thumb rule, forces due to both wires will be opposite in direction. Since no net force acts on the wire, the forces are equal in magnitude. Therefore, from eq (1) and eq (2), we get,
$\begin{align}
  & \dfrac{{{\mu }_{0}}\times 1\times I}{2\pi x}=\dfrac{{{\mu }_{0}}\times 2\times I}{2\pi (0.1+x)} \\
 & \Rightarrow \dfrac{1}{x}=\dfrac{2}{0.1+x} \\
 & \therefore x=0.1m \\
\end{align}$

The wire is $0.1m$ from the first wire away from the second, so the correct option is (C).

Note:
The right hand thumb rule gives the direction of current as well as force due to magnetic field of a current carrying wire. It states that if the thumb represents the direction of force, then the fingers represent the direction of current as well as the force. Force acting on a current carrying wire is basically a summation of the forces acting on the charges flowing through it.