Question

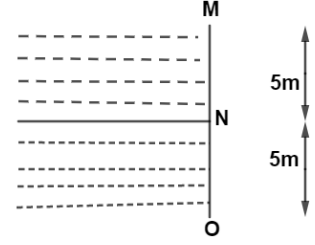
Two liquids of densities ${\rho _1}$ and ${\rho _2}({\rho _2} = 2{\rho _1})$ are filled up behind a square wall of side $10m$ as shown in figure. Each liquid has a height of $5m$ the ratio of forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not moving)

A. $\dfrac{1}{3}$
B. $\dfrac{1}{4}$
C. $\dfrac{1}{2}$
D. $\dfrac{2}{3}$

Answer 1

Hint: In order to solve this question we need to understand buoyant force. We know from Newton’s laws of motion that any material opposes the change in its state so when water or any liquid is being pressed by some object then water opposes this behavior in its change of state and hence it exerts an upward or buoyant force on the volume of object inside liquid, this is known as buoyancy.

Complete step by step answer:
Here we can use formula: $P = \rho gh \to (i)$
Where, $P$ is pressure, $g$ is acceleration due to gravity, “$h$” is height of the water column above the point at which pressure acts and $\rho $ is the density of liquid.
Also we would use, $F = PA \to (ii)$
Where, $F$ is force, $P$ is pressure applied and $A$ is area.

Considering Pressure at different point shown in figure,

So at A point there is no liquid above it so pressure at “A” point is, ${P_A} = 0$.
Similarly at “B” point height of liquid above it is, $h = 5m$.
And the liquid of density ${\rho _1}$.
So the pressure at “B” point is,
${P_B} = 5{\rho _1}g$ using $(i)$
Similarly at “C” point height of liquid of density ${\rho _1}$ is ${h_1} = 5m$ and height of density of liquid ${\rho _2}$ is, ${h_2} = 5m$

Using $(i)$ we get pressure at C point equals to,
${P_C} = {\rho _1}g{h_1} + {\rho _2}g{h_2}$
Using ${\rho _2} = 2{\rho _1}$
Putting values we get,
${P_C} = 5g{\rho _1} + 10g{\rho _1}$
$\Rightarrow {P_C} = 15g{\rho _1}$
So the pressure on wall MN is, ${F_A} = \dfrac{{({P_A} + {P_B})}}{2}A$ using $(ii)$
Putting values we get, ${F_A} = \dfrac{{5g{\rho _1}}}{2}A$
Also pressure on wall ON is, ${F_B} = \dfrac{{({P_B} + {P_C})}}{2}A$
Putting values we get, ${F_B} = \dfrac{{20g{\rho _1}}}{2}A$
So, $\dfrac{{{F_A}}}{{{F_B}}}$ is given by,
$\dfrac{{{F_A}}}{{{F_B}}} = \dfrac{{\dfrac{{5g{\rho _1}}}{2}A}}{{\dfrac{{20g{\rho _1}}}{2}A}}$
$\therefore \dfrac{{{F_A}}}{{{F_B}}} = \dfrac{1}{4}$

So the correct option is B.

Note: It should be remembered that pressure applied at any point is only applied by liquid above it and not by liquid below it also acceleration due to gravity is only acceleration that is applied here if the liquid is under some acceleration in any other direction the pressure applied would be changed. Also viscosity is defined as force of friction between layers of liquid.