Question

Two lamp posts are 60 meters apart, and the height of the one is double that of the other. From the middle of the line joining their feet, an observer finds the angular elevation of their top to be complimentary. Find the height of each lamp.
$
  (a){\text{ 52}}{\text{.63 m; 85}}{\text{.22 m}} \\
  (b){\text{ 46}}{\text{.53 m; 71}}{\text{.39 m}} \\
  (c){\text{ 20}}{\text{.63 m; 22}}{\text{.32 m}} \\
  (d){\text{ 21}}{\text{.21 m; 42}}{\text{.42 m}} \\
 $

Answer 1

Hint: In this height and distance problem the distance between two lamps is given and the relation between the heights of two lamps is also given. Now it is given that an observer finds the angular elevation of their top to be complimentary. Thus using the definition of complementary angles if one angle is $\theta$ then the other must be $90-\theta$ as the sum of complementary angles Is 90. Use this concept to get the answer.

Complete step-by-step answer:

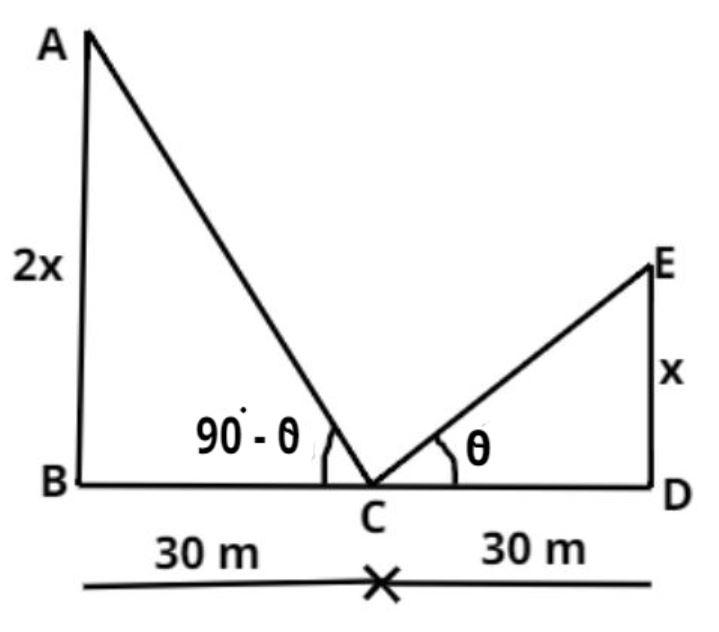
It is given that the length of one lamp post is double to another.
So, let the length of one lamp post be 2x m (see figure).
And the length of the other lamp post is x m (see figure), which satisfies the condition.
Now it is given that the observer is at the middle of the line joining the feet (say at C).
And it is given that two lamp posts are 60 meters apart.
$ \Rightarrow BC = CD = \dfrac{{BD}}{2} = \dfrac{{60}}{2} = 30{\text{ m}}$ (See figure).
Now it is also given the angular elevation of their top to be complementary.
I.e. $\angle BCA + \angle DCE = {90^ \circ }$.
Let angle $\angle DCE = \theta $
Therefore $\angle BCA = {90^ \circ } - \theta $
Now in triangle ABC
$\tan \left( {{{90}^ \circ } - \theta } \right) = \dfrac{{{\text{Perpendicular}}}}{{{\text{base}}}} = \dfrac{{2x}}{{30}}$
As we know $\tan \left( {{{90}^ \circ } - \theta } \right) = \cot \theta $ so, apply this property then we have,
$ \Rightarrow \cot \theta = \dfrac{{2x}}{{30}}$
Now as we know $\cot \theta = \dfrac{1}{{\tan \theta }}$ so, apply this property then we have,
$ \Rightarrow \tan \theta = \dfrac{{30}}{{2x}}$ …………….. (1)
Now in triangle DCE
$\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{base}}}} = \dfrac{x}{{30}}$
$ \Rightarrow \tan \theta = \dfrac{x}{{30}}$ ………………………….. (2)
Now in equation (1) and (2) L.H.S is the same, therefore R.H.S also should be the same.
So, equate R.H.S then we have,
$ \Rightarrow \dfrac{x}{{30}} = \dfrac{{30}}{{2x}}$
Now simplify this equation then we have,
$ \Rightarrow 2{x^2} = 900$
Now divide by 2 and take square root then we have,
$
   \Rightarrow {x^2} = \dfrac{{900}}{2} = 450 \\
   \Rightarrow x = \sqrt {450} = 21.21{\text{ m}} \\
$
So the height of second lamp post is $2x = 2 \times 21.21 = 42.42{\text{ m}}$
Hence option (d) is correct.

Note: Whenever we face such types of problems the key concept here is to use the basic trigonometric ratios in the specific triangles. The diagrammatic representation of the data provided in the question helps in better understanding of geometry and thus helping you through to get the right answer.