Question

Two intersecting lines cannot be parallel to the same line’ is stated in the form of:
A) An axiom
B) A definition
C) A postulate
D) A proof

Answer 1

Hint:
We know about the meaning of parallel lines; parallel lines means the line which cannot intersect to each other, if both the lines are in a plane. If two lines are the intersecting lines it means the lines never are parallel to each other in a plane.

Complete step by step solution:
Two intersecting lines cannot be parallel to the same line. For example, we draw three lines like P, Q, and R which is given below:

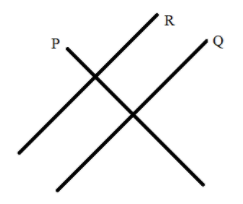
From the above figure we see that the line P and line Q are intersecting and line R is parallel to line Q but the line Q is not parallel to line P. intersecting lines means that the one solution. Therefore, intersecting lines never parallel to the same line. Here the given statement, two intersecting lines cannot be parallel to the same line is true and which is defined by an axiom word.

Hence, the option (A) is correct.

Additional Information:
It should be known that we are talking about lines in a plane not lines in different planes. If lines intersect then they meet at one point or infinite points. It cannot be possible that two lines are intersecting at two points.

Note:
Here you should know the difference between intersecting lines and parallel lines. Intersecting lines are lines that, at some point, cross or meet. Parallel lines, where two or more lines lie in the same plane and never intersect, are parallel.