Question

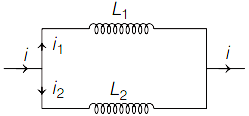
Two inductors \[{L_1}\]​ and \[{L_2}\]​ are connected in parallel and a time-varying current flows as shown in figure. Then the ratio of currents \[{i_1}/{i_2}\]​ at any time \[t\] is

A.\[\dfrac{{{L_1}}}{{{L_2}}}\]
B.\[\dfrac{{{L_2}}}{{{L_1}}}\]
C.\[{\dfrac{{{L_1}^2}}{{({L_1} + {L_2})}}^2}\]
 D.\[{\dfrac{{{L_2}^2}}{{({L_1} + {L_2})}}^2}\]

Answer 1

Hint: An inductor is an electronic component that stores energy in the form of a magnetic field. The inductor opposes the alternating current flowing through it. Inductors can be used in the circuit as series or parallel connections. This causes a generation of an emf due to a change of current in the circuit. The equivalent inductance in the parallel is less than the inductance of the individual inductor.

Complete answer:
Given that the two inductors are connected in parallel connection. Also, a time-varying current flows through the circuit.
Due to the self-inductance, a back emf is \[{E_1}\] and \[{E_2}\] will be generated in the first and second inductor.
The induced emf in the inductor can be written in terms of the self-inductance as,
For inductor \[{L_1}\]; \[{E_1}\]\[ = {L_1}\dfrac{{d{i_1}}}{{dt}}\]
For inductor \[{L_2}\]; \[{E_2} = {L_2}\dfrac{{d{i_2}}}{{dt}}\]
We know that when the inductors are connected in parallel the potential difference between the inductors is the same. Therefore equating the emf induced by both the inductors we get,
\[{L_1}\dfrac{{d{i_1}}}{{dt}} = {L_2}\dfrac{{d{i_2}}}{{dt}}\]
\[ \Rightarrow {L_1}d{i_1} = {L_2}d{i_2}\]
\[ \Rightarrow {L_1}{i_1} = {L_2}{i_2}\]
\[ \Rightarrow \dfrac{{{i_1}}}{{{i_2}}} = \dfrac{{{L_2}}}{{{L_1}}}\]
The ratio of currents \[{i_1}/{i_2}\]​ at any time \[t\] is, \[\dfrac{{{L_2}}}{{{L_1}}}\].

Therefore the correct option is B.

Note:
When we connect the inductors in series the total inductance in the circuit is always greater than any one of the individual inductors’ inductances. This is because when the inductors are connected in series the total voltage drop due to the change in the current will be additive with each inductor this in turn will create a greater total voltage than the individual inductors. On the other hand, when the inductors are connected in parallel the total inductance of the circuit will be less than any one of the individual inductors. This is because the current through each parallel inductor will be a fraction of the total current and the voltage across each parallel inductor will be equal. Therefore a change in total current will eventually result in lesser voltage drop across the parallel circuits than for individual inductors.