Question

Two inductors each of inductance L are connected in parallel. One more inductor of value 5mH is connected in a series of this configuration then the effective inductance is 15 mH. The value of L is ---- mH.
A. 10
B. 5.0
C. 2.5
D. 20

Answer 1

Hint: Find the effective inductance of the inductance in parallel in terms of L and then find the value of the effective inductance after the addition of the one more inductor using the formulae of the effective inductance in case of series and parallel inductors.

Complete step by step solution:
Now we know the value of the effective inductance when the inductors are in parallel is given as
$\dfrac{1}{L_{eff}} = \dfrac{1}{L_1} + \dfrac{1}{L_2}$
We get the value of the effective inductance in case of the inductors arranged in series as:
$L_{eff} = L_1 + L_2$
We now can solve the problem quickly, first we will draw a diagram for the situation given:

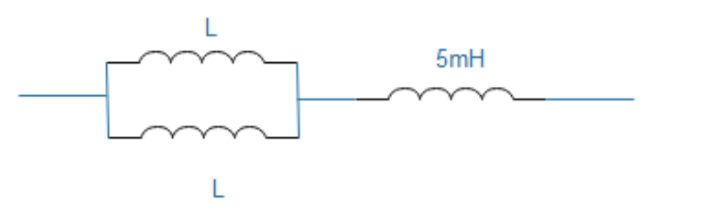
We can now implement the above formula to get the value of effective inductance:
We are given that the two inductance of value L are connected in parallel so the effective value of inductance $\dfrac{1}{L_{eff}} = \dfrac{1}{L} + \dfrac{1}{L} = \dfrac{2}{L} $
So, we get $L_{eff} = \dfrac{L}{2}$
Now we have found the effective value of the one part of the circuit we get the value of the final effective value of the inductance by adding the value connected in series
So, we get
$L_{eff} = \dfrac{L}{2} + 5 \times 10^{-3}$
We are given the effective value of the combination as 15 mH
So we get the value of the L by equating the above as below:
$15 \times 10^{-3} = \dfrac{L}{2} + 5 \times 10^{-3} $
We get that $\dfrac{L}{2} = (15 - 5 ) \times 10^{-3} $
We get $L = 2 \times 10 \times 10 ^{-3}$
L = 20 mH
Hence, we found the effective value of the inductance and then found the required value of L as 20 mH.

Note: The effective value of the inductance can be calculated in a similar fashion as we do calculate in case of resistors but it is not the same case in case of capacitors. For the capacitors, we use the parallel form for the effective series resistance series form for the effective parallel capacitance.
So, we need to take care of that if we are given a combination of capacitors.