
Two identical positive charges are placed on the $y$ axis at $y=-a$ and $y=+a$. The variation of $V$ (electric potential) along $x$ axis is shown by graph:
A.
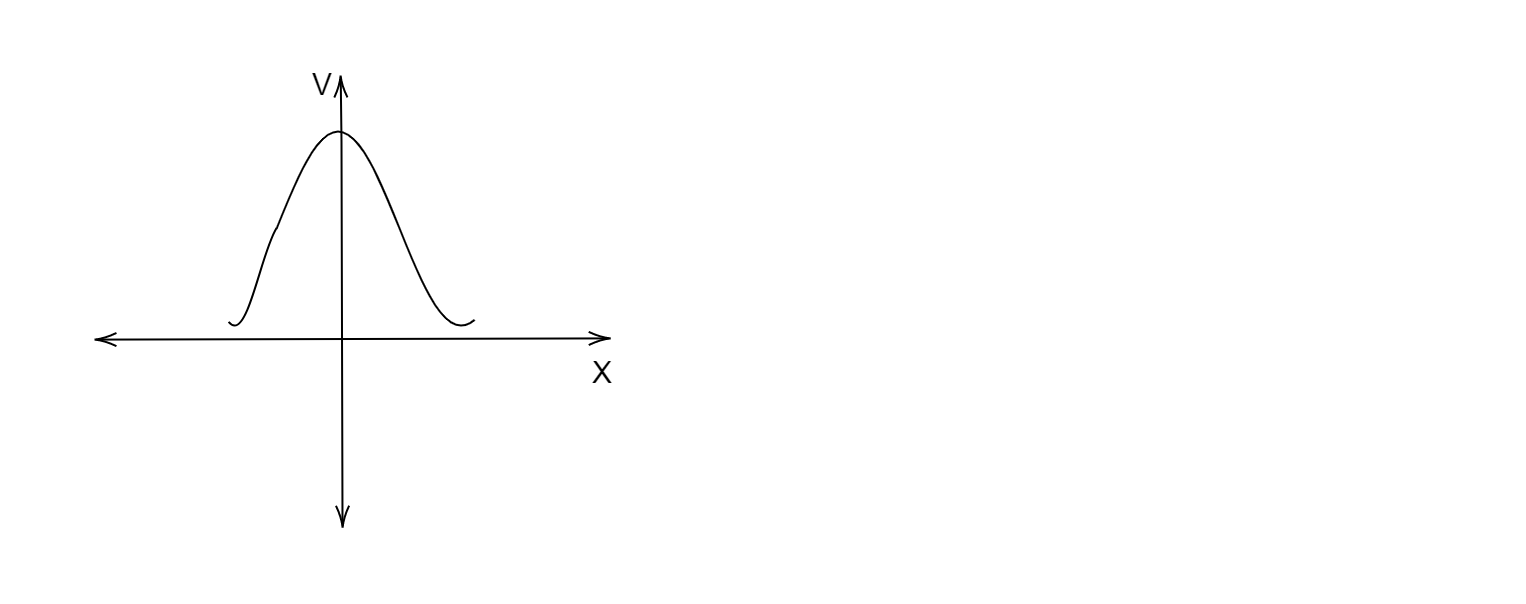
B.

C.
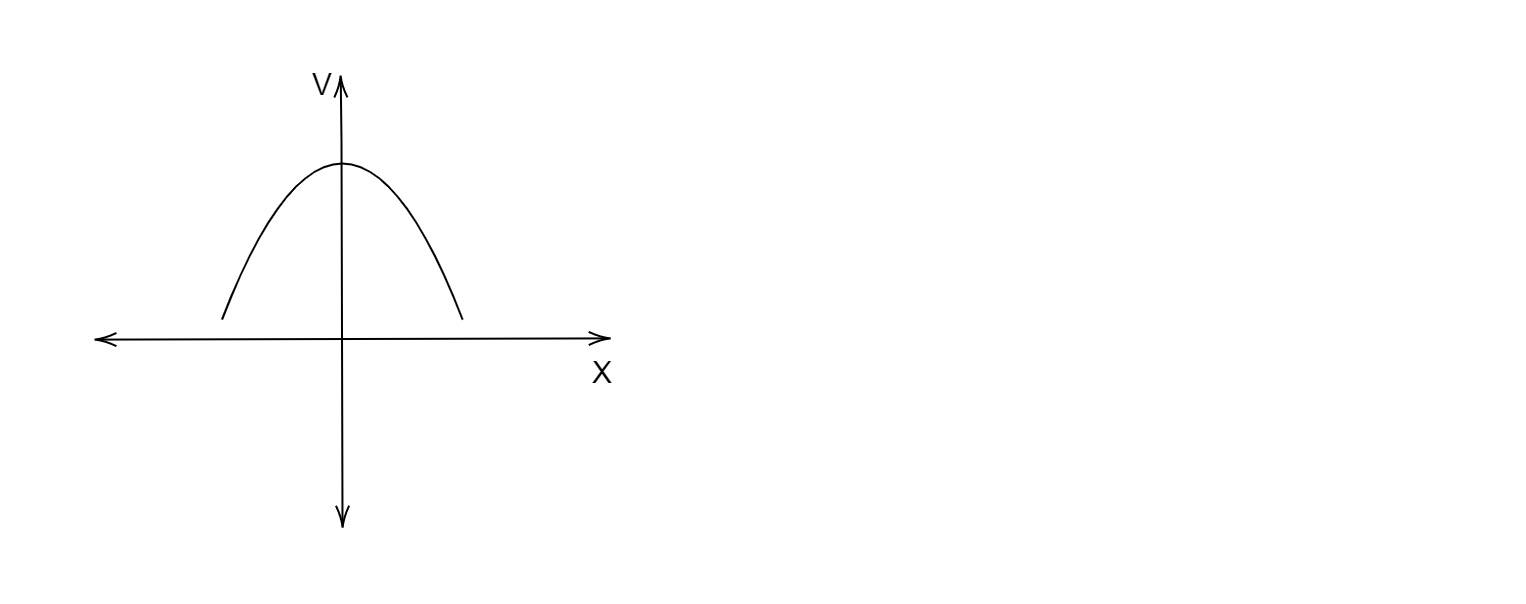
D.
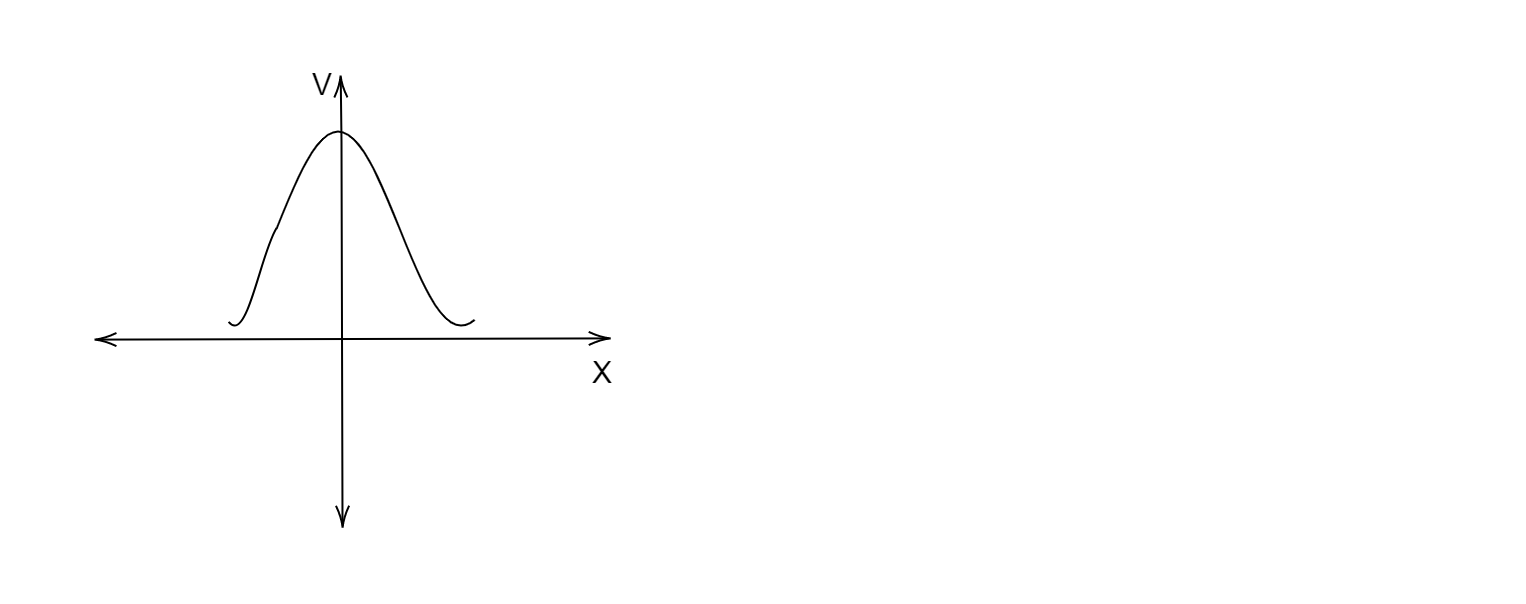

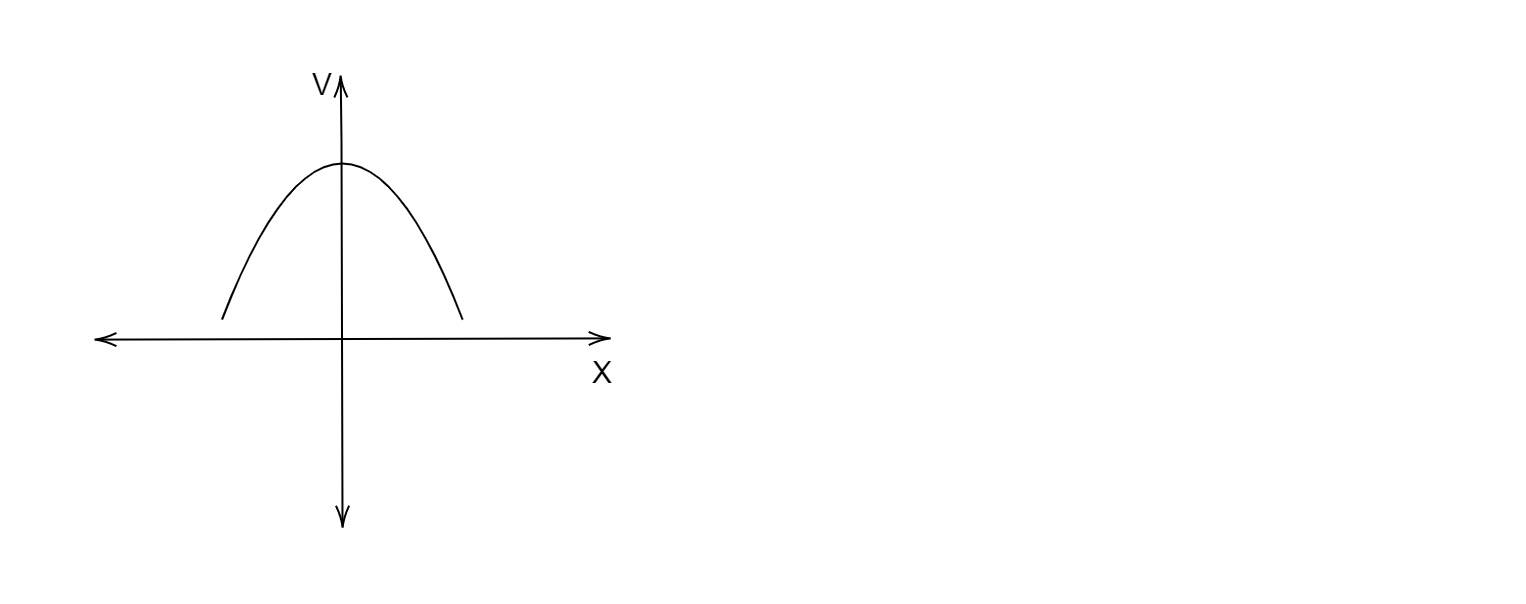
Answer
536.1k+ views
Hint: To know about the variation of electric potential along the $x$ axis can be found out by calculating electric potential at different points on the $x$ axis. We can calculate the electric potential at a random point on the $x$ axis first and then use it to find the variation of electric potential.
Complete answer:
Let us first consider a random point on the $x$ axis. Let the random point at which we will find the electric potential be at the point $(x,0)$ and let us call it $P$.
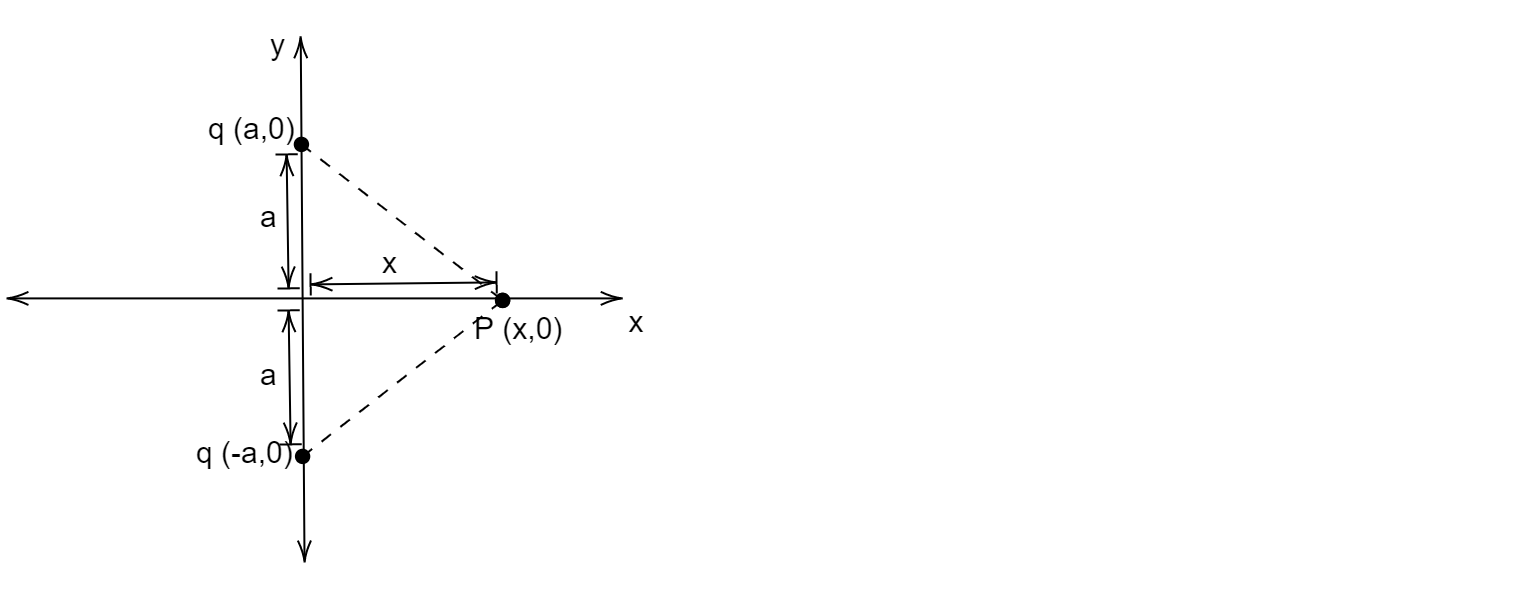
The distance $d$ of the point $P$ from the two identical positive charges can be found out by Pythagorean theorem:
$d=\sqrt{{{a}^{2}}+{{x}^{2}}}$
The electric potential at point $P$ due to the positive charge placed at $y=-a$ will be:
${{V}_{1}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}$
The electric potential at point $P$ due to the positive charge placed at $y=+a$ will be:
${{V}_{2}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}$
The total electric potential at point $P$ due to both the positive charges will be:
$\begin{align}
& {{V}_{total}}={{V}_{1}}+{{V}_{2}} \\
& {{V}_{total}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}+\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\
& {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\
\end{align}$
At origin, when $x=0$, the total electric potential will be:
$\begin{align}
& {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{0}^{2}}}} \\
& {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}}} \\
& {{V}_{total}}=\dfrac{2kq}{a} \\
\end{align}$
When $x\to \infty $, the total electric potential will be:
$\begin{align}
& {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\
& {{V}_{total}}=\dfrac{2kq}{x\sqrt{\dfrac{{{a}^{2}}}{{{x}^{2}}}+\dfrac{{{x}^{2}}}{{{x}^{2}}}}} \\
& {{V}_{total}}=\dfrac{2kq}{x\sqrt{0+1}} \\
& {{V}_{total}}=\dfrac{2kq}{x} \\
& {{V}_{total}}\to 0 \\
\end{align}$
Now we need to find the graph that matches the value of the electric potential that we found out for electric potential at $x=0$ and $x\to \infty $. If we observe carefully, then graph $A$ acquires a maximum value at $x=0$ and a minimum value at $x\to \infty $.
Therefore, the correct option is $A$.
Note:
Students might get confused between option $A$ and option $C$ but we must also see that the electric potential is inversely proportional to the distance on $x$ axis, therefore the graph must be a rectangular hyperbola, thus option $A$ must be correct.
Complete answer:
Let us first consider a random point on the $x$ axis. Let the random point at which we will find the electric potential be at the point $(x,0)$ and let us call it $P$.
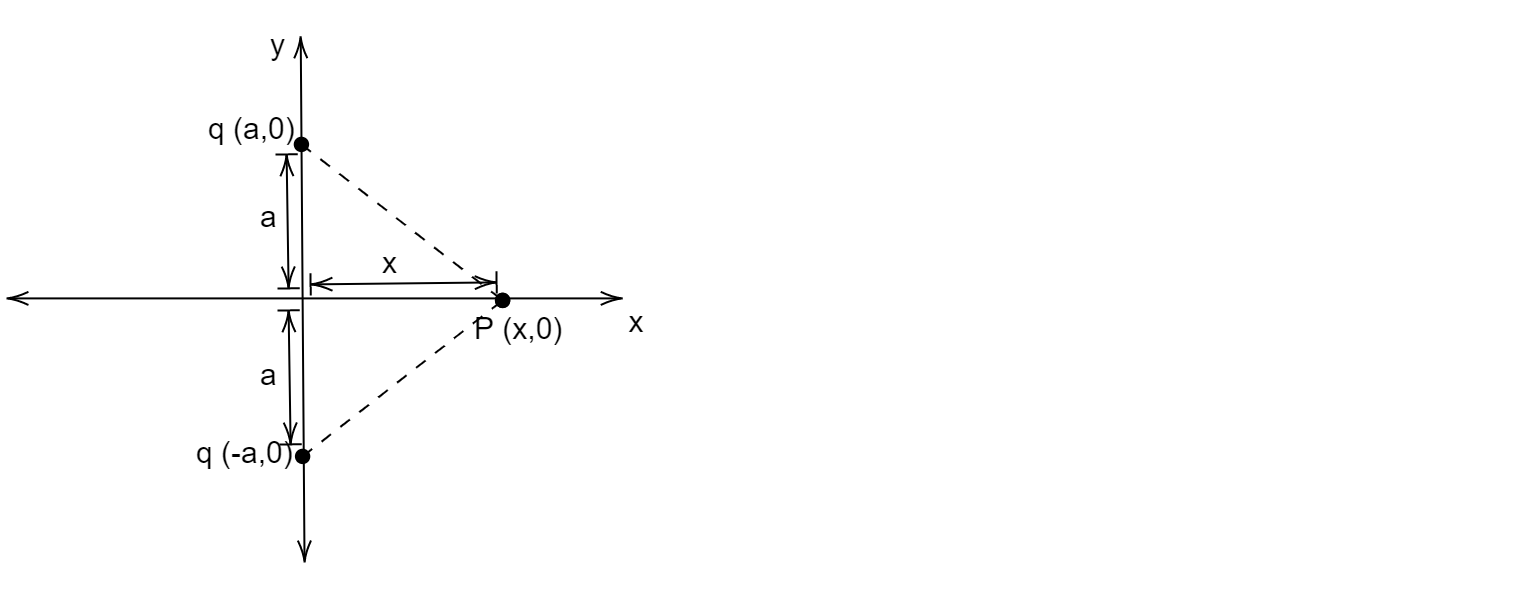
The distance $d$ of the point $P$ from the two identical positive charges can be found out by Pythagorean theorem:
$d=\sqrt{{{a}^{2}}+{{x}^{2}}}$
The electric potential at point $P$ due to the positive charge placed at $y=-a$ will be:
${{V}_{1}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}$
The electric potential at point $P$ due to the positive charge placed at $y=+a$ will be:
${{V}_{2}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}$
The total electric potential at point $P$ due to both the positive charges will be:
$\begin{align}
& {{V}_{total}}={{V}_{1}}+{{V}_{2}} \\
& {{V}_{total}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}+\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\
& {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\
\end{align}$
At origin, when $x=0$, the total electric potential will be:
$\begin{align}
& {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{0}^{2}}}} \\
& {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}}} \\
& {{V}_{total}}=\dfrac{2kq}{a} \\
\end{align}$
When $x\to \infty $, the total electric potential will be:
$\begin{align}
& {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\
& {{V}_{total}}=\dfrac{2kq}{x\sqrt{\dfrac{{{a}^{2}}}{{{x}^{2}}}+\dfrac{{{x}^{2}}}{{{x}^{2}}}}} \\
& {{V}_{total}}=\dfrac{2kq}{x\sqrt{0+1}} \\
& {{V}_{total}}=\dfrac{2kq}{x} \\
& {{V}_{total}}\to 0 \\
\end{align}$
Now we need to find the graph that matches the value of the electric potential that we found out for electric potential at $x=0$ and $x\to \infty $. If we observe carefully, then graph $A$ acquires a maximum value at $x=0$ and a minimum value at $x\to \infty $.
Therefore, the correct option is $A$.
Note:
Students might get confused between option $A$ and option $C$ but we must also see that the electric potential is inversely proportional to the distance on $x$ axis, therefore the graph must be a rectangular hyperbola, thus option $A$ must be correct.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




