Question

Two identical pendulums of length $'l'$ have masses $'m'$ at their ends. Both masses are joined by a light massless spring of spring constant $'s'$ at a distance with zero displacement. If both pendulums oscillate in opposite directions, then the angular frequency $\omega $ of coupled system is?

Answer 1

Hint:Here, you are given two pendulums which are connected using a spring of spring constant $'s'$ and the system is set for an oscillation with pendulums moving in opposite directions. You are asked to find the frequency with which the pendulums will oscillate. In order to solve the question, focus on only one pendulum and write the equations of motion. Here, you can assume that the oscillation is symmetric, meaning that the distance moved by one bob is equal to the distance moved by the other.

Complete step by step answer:
First, we draw the figure of the system at some intermediate stage.

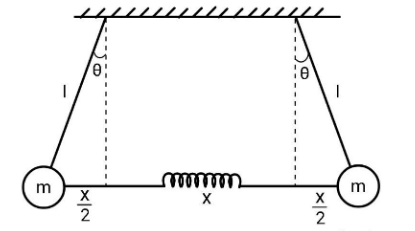
The above figure is a snapshot of the motion of the two pendulums. Here, $x$ is the elongation produced in the spring and as we already assumed that the motion is symmetric, elongation produced due to each pendulum will be $\dfrac{x}{2}$. As said previously, we will focus on only one pendulum and let that pendulum be the left one. Now, let us write the restoring torque on the left bob about the point of suspension of the left pendulum.

Forces acting on the bob are:
(1) force due to gravity acting vertically downward, $mg \downarrow $
(2) force of spring acting along spring towards right, $kx \to $.
Therefore, $\tau = - \left[ {\left( {mg} \right)\left( {\dfrac{x}{2}} \right) + \left( {kx} \right)\left( {l\cos \theta } \right)} \right]$.
The thing to consider here is that the oscillation is small, meaning that the angle $\theta $ is small. For small angle $\theta $, we have $\sin \theta \approx \theta $ and $\cos \theta \approx 1$. We will use these approximations.

From figure, you can see that $\sin \theta = \dfrac{{\dfrac{x}{2}}}{l} = \dfrac{x}{{2l}}$, as $\sin \theta \approx \theta $, we have $\theta = \dfrac{x}{{2l}}$.
So, we can write torque as,
$\tau = - \left[ {\left( {mg} \right)\left( {\dfrac{{2l\theta }}{2}} \right) + \left( {k2l\theta } \right)\left( l \right)} \right] \\
\Rightarrow\tau = - \left( {mgl + 2k{l^2}} \right)\theta \\ $
Also, \[\tau = I\alpha \], where $I$ is the moment of inertia of the bob and is given by $I = m{l^2}$.
$m{l^2}\alpha = - \left( {mgl + 2k{l^2}} \right)\theta \\
\Rightarrow\alpha = - \left( {\dfrac{{\,mgl + 2k{l^2}}}{{m{l^2}}}} \right)\theta \\
\Rightarrow\alpha = - \left( {\dfrac{g}{l} + \dfrac{{2k}}{m}} \right)\theta \\
\Rightarrow\alpha = - {\omega ^2}\theta \\
\therefore\omega = \sqrt {\dfrac{g}{l} + \dfrac{{2k}}{m}} \\ $
Therefore, the angular frequency $\omega $ of the coupled system is $\sqrt {\dfrac{g}{l} + \dfrac{{2k}}{m}}$.

Note: We have compared the final obtained equation with the standard equation of SHM so keep this thing in mind. Also keep in mind that the general approach to solve this question would be to take elongation produced by one bob be ${x_1}$ and by other be ${x_2}$, now you would have to write equations for both the bob and obtain combined equations of \[{x_1}\& {x_2}\]. In the general approach you will get two angular frequency, one will be of bobs oscillating in same direction and the other will be bobs oscillating in opposite direction, in this case also you will get the same value of angular frequency as derived by us assuming symmetric oscillation.