Question

Two identical ladders are arranged as shown in the figure, resting on a horizontal surface. Mass of each ladder is M and length L. A block of mass m hangs from the apex point P. If the system is in equilibrium, find direction and magnitude of friction?

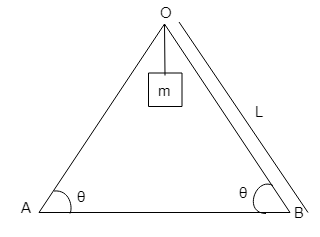
Answer 1

Hint: In order to solve this question, first we will draw the free body diagram and find the force equations for the two ladders. Then we will form an equation by balancing the torque which is acting on the point O and by putting the value from the force equations in this equation, we get the correct answer.

Complete step-by-step answer:
First we need to find out all the forces acting on the two ladders, in order to do so, we need to draw the free body diagram. So, the free body diagram of the two ladders are:

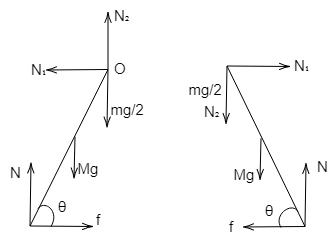
(Image source: Self drawn on mathcha)
We know that all the ladders are in equilibrium. So,
$\sum {{F_x}} = 0$
$\sum {{F_y}} = 0$
And from this above equations, we can say that,
${\tau _{net}} = 0$
For the right ladder,
${N_2} + \dfrac{{mg}}{2} + Mg = N....(1)$
${N_1} = f......(2)$
Similarly, for the left rod, we get,
${N_2} + N = Mg + \dfrac{{mg}}{2}......(3)$
On adding equation (1) and (3), we get,
${N_2} + N + {N_2} + \dfrac{{mg}}{2} + Mg = Mg + \dfrac{{mg}}{2} + N$
On cancelling the common terms on both the sides, we get,
${N_2} + {N_2} = 0$
$2{N_2} = 0$
${N_2} = 0......(4)$
On putting the value of equation (4) in equation (1), we get,
$N = \dfrac{{mg}}{2} + Mg......(5)$
Now, on balancing the toques acting about the point O, we get,
\[Mg\dfrac{L}{2}\cos \theta + fL\sin \theta = NL\cos \theta \]
On cancelling the common terms on both the sides, we get,
\[\dfrac{{Mg}}{2}\cos \theta + f\sin \theta = N\cos \theta \]
On putting the value in the above equation from equation (5),
\[\dfrac{{Mg}}{2}\cos \theta + f\sin \theta = \dfrac{{mg}}{2}\cos \theta + Mg\cos \theta \]
\[f\sin \theta = \dfrac{{mg}}{2}\cos \theta + \dfrac{{Mg}}{2}\cos \theta \]
On taking the term $\sin \theta $ on the other side, we get,
\[f = \left( {\dfrac{{mg}}{2} + \dfrac{{Mg}}{2}} \right)\cot \theta \]
\[f = \left( {\dfrac{{m + M}}{2}} \right)g\cot \theta \]
So, the magnitude of the force of friction is \[f = \left( {\dfrac{{m + M}}{2}} \right)g\cot \theta \] and the direction of the force of friction is horizontally inwards.

Note: The value of static friction changes as the magnitude of the force applied changes while kinetic friction is very much independent of the magnitude of the force which is applied. Static friction is the force which stops an object from moving whereas kinetic friction is the force which is offered to something which is already in motion.